查询处理的基本步骤
- 语法分析与翻译
- 优化
- 执行
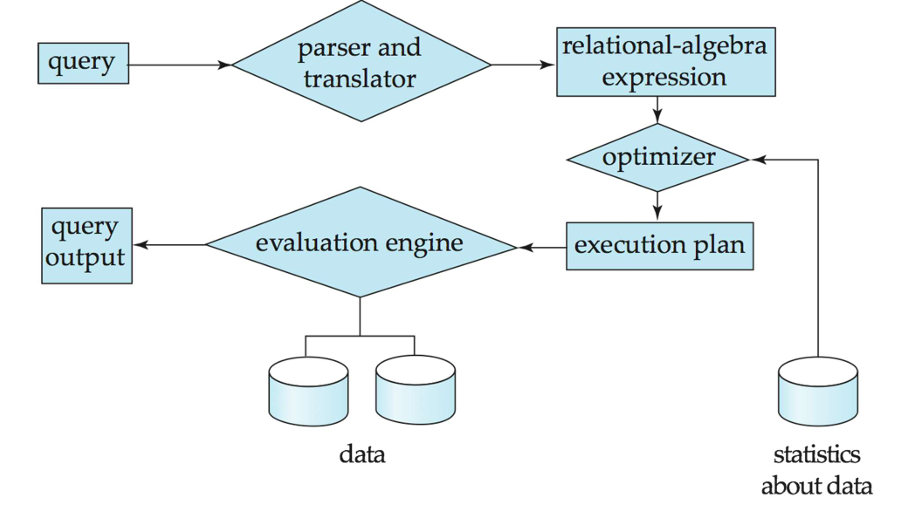
语法分析与翻译
- 将查询转换为内部形式,然后将其转换为关系代数。
- 解析器检查语法,验证关系。
执行
- 查询执行引擎接收查询执行计划,执行该计划,并返回查询的结果。
优化
- 关系代数表达式可能有许多等价的表达式。
例如, - 每个关系代数操作可以使用多种不同的算法进行执行。相应地,关系代数表达式可以以多种方式进行执行。指定详细执行策略的注释表达式称为
执行计划或计算计划(evaluation-plan)。 - 例如,可以使用薪水索引来查找薪水小于 75000 的讲师,或者执行完整的关系扫描并丢弃薪水大于等于 75000 的讲师。
查询优化(Query Optimization):在所有等价的执行计划中选择成本最低的计划。- 成本是使用数据库目录中的统计信息进行估算的。
- 例如,每个关系中的元组数量、元组大小等。
衡量查询开销
- 成本通常以回答查询所需的总耗时来衡量。
- 许多因素会影响时间成本,包括磁盘访问、CPU 或网络通信。
- 通常,磁盘访问是主要的成本,并且相对容易估计。通过考虑以下因素进行测量:
- 寻道次数 * 平均寻道成本
- 读取的块数 * 平均块读取成本
- 写入的块数 * 平均块写入成本
- 写入块的成本大于读取块的成本,因为在写入后需要将数据读回来以确保写入成功。
- 为简单起见,我们只使用磁盘的块传输数量和寻道次数作为成本度量。
- 成本为 b 个块传输加上 S 次寻道的时间:
- 为简单起见,我们忽略了 CPU 成本。实际系统会考虑 CPU 成本。
- 我们在成本公式中不包括将输出写入磁盘的成本。
- 通过使用额外的缓冲空间,可以减少磁盘 IO 的次数。
- 在最好的情况下,所有数据都可以读入缓冲区,不需要再次访问磁盘。
- 在最坏的情况下,我们假设缓冲区只能容纳少量的数据块,大约每个关系一个数据块。
- 通常我们假设最坏情况。
选择操作
| 算法 | 开销 | 原因 | |
|---|---|---|---|
| A1 | 线性搜索 | 一次初始搜索加上 | |
| A1 | 线性搜索,码属性等值比较。 | 平均情形 | 因为最多一条记录满足条件,所以只要找到所需的记录,扫描就可以终止。在最坏的情况下,仍需要 |
| A2 | (其中 | ||
| A3 | 树的每层一次搜索,第一个块一次搜索。 | ||
| A4 | 这种情形和主索引相似 | ||
| A4 | (其中 | ||
| A5 | 和 A3,非码属性等值比较情形一样 | ||
| A6 | 和 A4,非码属性等值比较情形一样 |
A1(线性搜索)
- 算法 A1(线性搜索):扫描每个文件块,并测试所有记录以确定它们是否满足选择条件。
- 成本估计 =
- 其中
- 其中
- 如果选择条件是基于关键属性,可以在找到记录后停止搜索。
- 成本 =
- 成本 =
- 无论选择条件如何、记录在文件中的排序如何、是否有索引可用,都可以使用线性搜索。
- 成本估计 =
- 注意:二分搜索通常没有意义,因为数据不是连续存储的,除非有可用的索引,而且二分搜索需要比索引搜索更多的寻道次数。
A2(主索引,基于关键字的相等性)
- 示例查询:select *from instructor where ID="007",其中 ID 是一个主索引;
- 索引访问成本:
- 文件访问成本:
- 总成本 =
A3(主索引,非关键字的相等性)
- 示例查询:select * from instructor where name="Einstein",其中 name 是一个主索引;
- 检索多个记录。
- 记录将位于连续的块上。
- 令 b 为包含匹配记录的块数。
| index | file | |
|---|---|---|
| seek | h | 1 |
| transfer | h | b |
- 访问索引树的开销:
- 访问记录的开销:
- Cost =
A4(辅助索引,非关键字的相等性)
- 示例查询:select *from instructor where name="Einstein",其中 ID 是主索引,name 是辅助索引。
- 索引访问成本:
- 文件访问成本:
- 匹配的记录可能位于不同的块上。
- 总成本 =
- 索引访问成本:
- 可能非常昂贵。
- 若在候选键上,则等值为 Cost =
| index | file | |
|---|---|---|
| seek | h | n |
| transfer | h | n |
A5(主索引,比较)
- 对于形如
- 示例查询:select *from instructor where ID <= "9999",ID 是主索引。
- 算法:对于
- 算法:对于
- 示例查询:select* from instructor where ID >= "9999",ID 是主索引。
- 算法:对于
- 算法:对于
A6(辅助索引,比较)
- 示例查询:select *from instructor where name >= "Einstein",其中 ID 是主索引,name 是辅助索引。
- 算法:对于
- 算法:对于
- 示例查询:
select* from instructor where name <= "Einstein",其中 ID 是主索引,name 是辅助索引。- 算法:对于
- 算法:对于
- 在任一情况下,获取所指向的记录
- 每个记录需要一个 I/O 操作
- 线性文件扫描可能更便宜。
排序(Sorting)
- 对不能全部放在内存中的关系的排序称为
外排序(external sorting)。 - 外排序中最常用的技术是
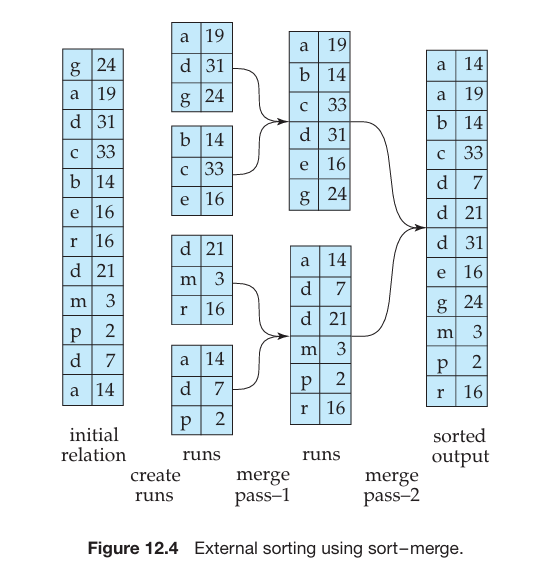
外部排序归并(external sort-merge)算法。下面讲述该算法。 - 令
步骤
- 第一阶段,建立多个排好序的归并段(run)。每个归并段都是排序过的,但仅包含关系中的部分记录。

- 第二阶段,对归并段进行归并。暂时假定归并段的总数

归并阶段的输出是已排序的关系。输出文件也被缓冲以减少写磁盘次数。上面的归并算法是对标准内存排序归并算法中的二路归并算法的推广;由于该算法对 N 个归并段进行归并,因此它称为
N路归并(N-way merge)。一般而言,若关系比内存大得多,则在第一阶段可能产生 M 个甚至更多的归并段,并且在归并阶段为每个归并段分配一个块是不可能的。在这种情况下,归并操作需要分多趟进行。由于内存足以容纳
最初那趟归并过程如下:头
此时,归并段的数目减少到原来的
外部归并排序的代价分析
- 令
- 在第一阶段要读入关系的每一数据块并写出,需要
- 初始归并段数为
- 每一趟归并会使归并段数目减少为原来的
- 对于每一趟归并,关系的每一数据块各读写一次,其中有两趟例外。
- 首先,最后一趟可以只产生排序结果而不写入磁盘。
- 其次,可能存在在某一趟中既没有读人又没有写出的归并段,例如,某一趟有
- 则关系外排序的磁盘块传输的总数:
- 归并阶段,如果每次从一个归并段读取
- 如果考虑到磁盘在写回块的间隔中的磁头移动,那么就需要为每趟归并加上总共
- 假设输出阶段也分配了
- 英文版教程 P549 页公式如下,它近似了一部分结果
连接操作(Join Operation)
- 有几种不同的算法可以实现连接操作:
- 嵌套循环连接(Nested-loop join)
- 块嵌套循环连接(Block nested-loop join)
- 索引嵌套循环连接(Indexed nested-loop join)
- 合并连接(Merge-join)
- 哈希连接(Hash-join)
- 选择算法时基于成本估计进行选择。
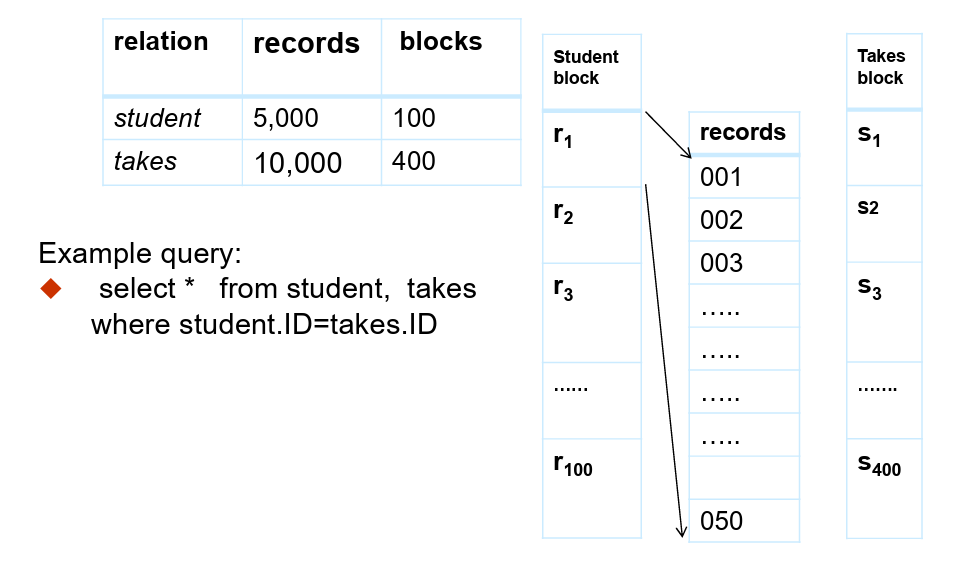
嵌套循环连接(Nested-loop join)
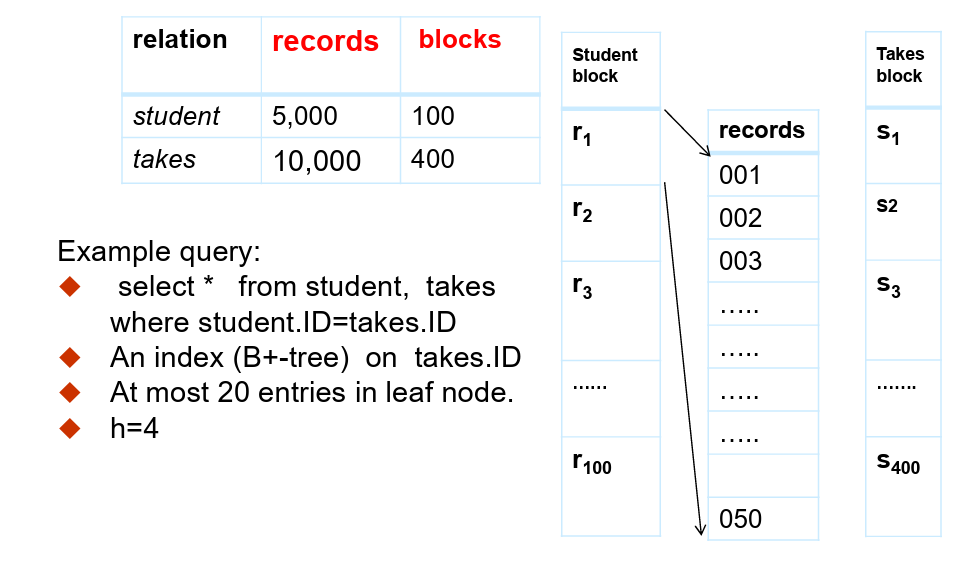
示例查询:
select * from student, takes where student.ID = takes.ID- 为了计算
- 对于关系
- 对于关系
- 检查元组
- 检查元组
- 对于关系
- 其中,
- 嵌套循环连接不需要索引,可以与任何类型的连接条件一起使用。
- 由于它检查两个关系中的每个元组对,所以开销较高。

开销
如果内存只能存储关系的一块的话,是最差情况,预估为:
| Worst case | r | s |
|---|---|---|
| transfers | ||
| seeks |
- 如果比较小的关系
| Best case | r | s |
|---|---|---|
| transfers | ||
| seeks | 1 | 1 |
块嵌套循环连接(Block nested-loop join)
对于关系
- 对于关系
- 对于块
- 对于块
- 检查元组
- 检查元组
- 对于块
- 对于块
- 对于关系
其实就是在前者的基础上多了一个读块的过程
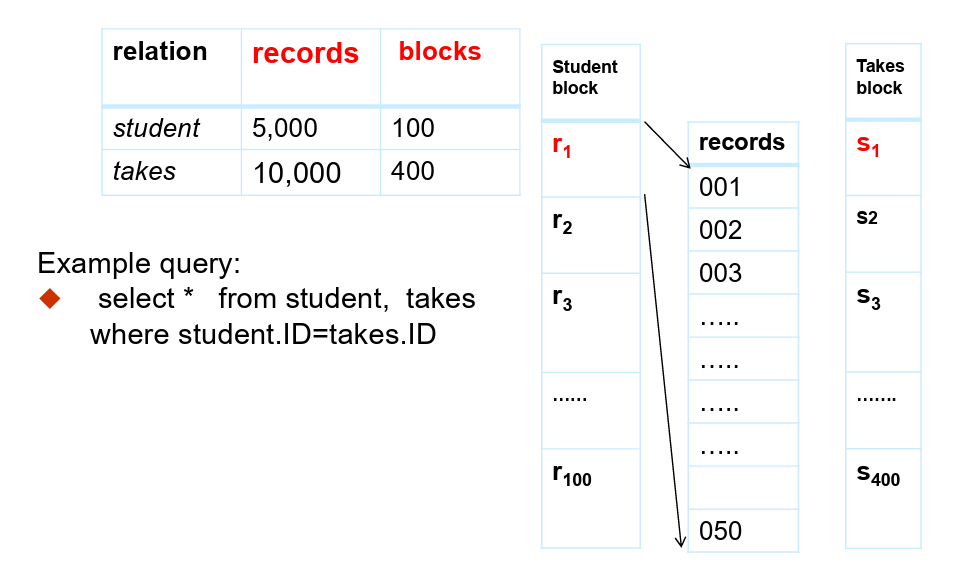
如果内存只能存储关系的一块的话,是最差情况,预估为:
| Worst case | r | s |
|---|---|---|
| transfers | ||
| seeks |
- 如果比较小的关系
| Best case | r | s |
|---|---|---|
| transfers | ||
| seeks | 1 | 1 |
- 显然,如果内存不能容纳任何一个关系,则使用较小的关系作为外层关系更有效。
改进方法
改进嵌套循环和块嵌套循环算法的方法有:
- 在块嵌套循环中,将
- 成本 =
- 如果等值连接属性形成内部关系的键,可以在第一次匹配时停止内部循环。
- 交替正向和反向扫描内部循环,以利用缓冲区中剩余的块(使用最近最少使用(LRU)替换策略)。
- 如果可用,使用内部关系的索引(下一部分)
:::
索引嵌套循环连接(Indexed nested-loop join)
如果连接是等值连接或自然连接,并且
内部关系的连接属性上存在索引,那么索引查找可以替代文件扫描。可以为计算连接而构建一个索引。
示例查询:
select * from student, takes where student.ID = takes.ID在
takes.ID上创建一个索引。算法:对于外部关系
| transfers | ||
| seeks |
最坏情况下:缓冲区只有一页的空间用于关系
连接的成本:
可以估计
如果在关系
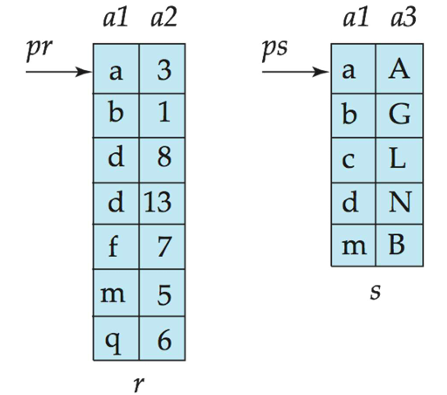
合并连接(Merge-join)
- 对两个关系的连接属性进行排序(如果它们尚未按连接属性排序)。
- 合并排序后的关系以进行连接操作。
连接步骤类似于排序-合并算法的合并阶段。 - 主要区别在于处理连接属性中的重复值-必须匹配具有相同连接属性值的每个对。
详细的算法请参考相关的书籍。
- 该方法仅适用于等值连接和自然连接。
- 假设对于连接属性的任何给定值,所有元组都适合内存,每个块只需要读取一次。
- 成本 = 排序成本 + 合并成本。
- 对于拥有
| r | s | |
|---|---|---|
| disk traverse | 1 | 1 |
| transfers | ||
| seeks |
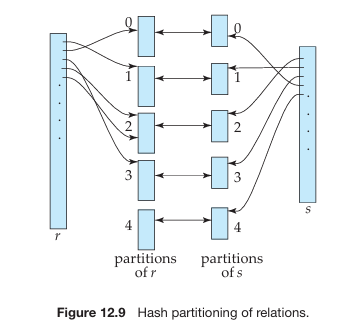
哈希连接(Hash-join)
- 适用于等值连接和自然连接。
- 使用哈希函数将两个关系的元组进行分区。
- 哈希函数
- 每个元组
- 每个元组
- 每个元组
注意:在书中,
- 满足连接条件的
- 如果该值被哈希到某个值
- 满足连接条件的
计算
- 使用哈希函数
- 类似地,对关系
- 对于每个分区
- 将
- 逐个从磁盘中读取
- 将
- 使用哈希函数
关系
构建输入(build input),而探测输入(probe input)。选择的值
- 通常,
- 探测关系
- 通常,
如果分区数
- 不是分区成
- 进一步使用不同的哈希函数对
- 在
- 很少需要:例如,对于块大小为 4 KB,对于小于 1GB 的关系和 2MB 内存大小,或者对于小于 36GB 的关系和 12MB 内存大小,不需要进行递归分区。
- 不是分区成
哈希连接开销
- 如果不需要进行递归分区:哈希连接的成本为
如果整个构建输入都可以放在主内存中,则不需要分区。
成本估计将降至 - 例如:
- 假设内存大小为 20 个块,其中
- 类似地,将
- 假设缓冲块为 3,则总成本(忽略部分填充块的写入成本)为:
- 假设内存大小为 20 个块,其中
表达式的执行(Evaluation of Expressions)
- 通过上面的内容,我们知道了对于单个操作的算法,我们有两个主要方法来执行整个表达式树:
- 物化计算(Materialization evaluation)
- 流水线(Pipeline)
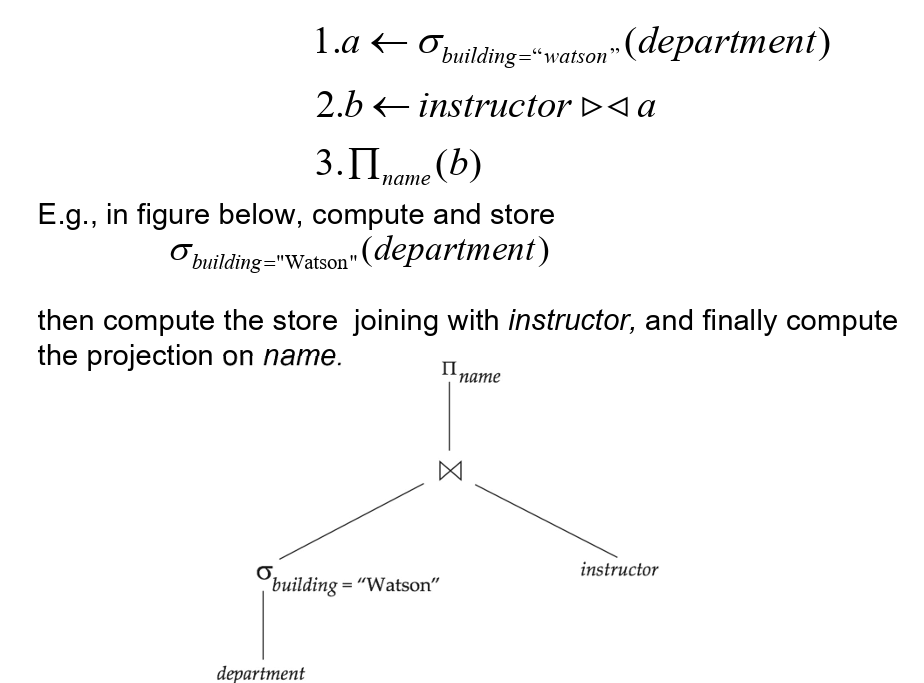
物化计算(Materialization evaluation)
- 逐个操作地执行查询,从最低级别开始。使用中间结果物化(Materailize)为临时关系,以执行下一级别的操作。
- 示例查询:
- Select name
- from instructor natural join department
- Where building=“watson”
- 这种方法经常是实用的
- 会带来额外的开销,因为要把中间结果写磁盘
- 双缓冲(double buffering)(即使用两个缓冲区,其中一个用于连续执行算法,另一个用于写出结果)允许 CPU 活动与 I/O 活动并行,从而提高算法执行速度。
流水线(Pipelining)
- 不储存中间结果,而是把中间结果直接传输到下一个要执行的操作上
- 管道传输不一定总是可行的,例如排序和哈希连接。为了使管道传输有效,使用评估算法,在接收到输入操作的元组时生成输出元组。
- 管道传输可以通过两种方式执行:
- 需求驱动(demand driven)
- 生产者驱动(producer driven)
- 另一种名称:拉取(pull)和推送(push)模型的管道传输。
- 在需求驱动或惰性(lazy)管道传输中:
- 系统会反复从顶层操作请求下一个元组。
- 每个操作根据需要从子操作请求下一个元组,以便输出其下一个元组。
- 在调用之间,操作必须维护“状态”,以便知道要返回什么。
- 在生产者驱动或渴望型(eager)管道传输中:
- 操作符会主动生成元组并将它们传递给它们的父级。
- 在操作符之间维护缓冲区,子操作符将元组放入缓冲区,父操作符从缓冲区中移除元组。
- 如果缓冲区已满,子操作符将等待,直到缓冲区有空间,然后生成更多的元组。
- 系统调度具有输出缓冲区空间和能够处理更多输入元组的操作符。
