Chapter3 语法分析

ChiChen原创大约 16 分钟

Chapter3 语法分析

正则表达式的能力有限，无法分析具体的语法细节(例如嵌套、 $a^{n} b^{n}$ 的n值)，与其等价的有穷自动机同理，因此引入了下推自动机和上下文有关、无关文法

大纲

语法分析的形式化——上下文无关文法
语法分析算法

上下文无关文法(CFG)

是用来描述一个编程语言的语法结构的文法
和正则表达式一样，可以表示递归的规则，而且更强大
是正则表达式的严格超集

Chomsky语言层级

Chomsky hierarchy	Production(产生式)	Explanation
unrestricted(type 0)(自然语言)	$α \to β V^{+} = V_{N} \cup V_{T}$ $其中 α \in V^{+}, β \in V^{*}$	无严格约束
context sensitive(type 1)(上下文有关文法)	$α A γ \to α β γ,$ $其中 α, γ \in V^{*}, A \in V_{N}, β \in V^{+}$	在不同的上下文中， $A$ 可能被不同的 $γ$ 替换
context free(type 2)(上下文无关文法)	$A \to β, A \in V_{N},$ $其中 β \in V^{*}$	在任何 $A$ 出现的地方都会被 $γ$ 替换
regular(type 3)(正则表达式)	$A \to a B o r A \to a$ $(其中 A, B A, b \in V_{N}, a \in V_{T})$	等价于正则表达式

$V_{N} 和 V_{T}$ 分别是非终止符号集(nonterminal)和终止符号(terminal)集，是由语言设计者设计的集合，终止符就是常说的token
如果一个符号由它自身定义( $a \to a$ 或 $i n t \to i n t$ )那么就是一个终止符号，通常是标点符号，如分号，括号等
如果一个符号有其定义的可再分的结构就是一个非终止符号( $l e t t e r \to [A - Z a - z]$ )，通常是句子，短语，表达式等
要注意， $A^{*}$ (Kleene闭包)是正则表达式特有的规则，CFG中没有，"|"在CFG中表示的是或，用来简化表示多个产生式，而不是正则表达式中的Union。
CFG文法规定的第一个文法的左部是开始符号，规定了该语言都满足的一个规则
一个处于较低层级的文法是上级文法的特例，例如RE就是一种特殊的CFG

形式化定义

\begin{matrix} C F G : G = (V_{T}, V_{N}, P, S) \\ V_{T} 是终止符集合 \\ V_{N} 是非终止符集合， V_{N} \cap V_{T} = \emptyset \\ P 是产生式集合，或称语法规则集，满足 A \to β A \in V_{N} 和 β \in (V_{N} \cup V_{T})^{*} \\ S 是初始符号， S \in V_{N} \end{matrix}

EBNF(Extended Backus-Naur form)

$\to$ ： $X \to Y_{1} Y_{2} Y_{3} . . . Y_{N}$ 表示 $X 可以用 Y_{1} Y_{2} Y_{3} . . . Y_{N}$ 来代替， $X \to ε$ 表示 $X$ 可以用空串代替，这种 $A \to α$ 被称为BNF表示法
简化表示：
1. 除非特殊说明，否则第一个产生式的左部就是初始符号
2. 用小写字母表示终止符号
3. 用大写字符或者 $< . . . >$ 表示非终止符号
4. 如果左部都为 $A$ 的一系列产生式 $A \to α_{2}, . . ., A \to α_{n},$ 可以简写为 $A \to α_{1} | α_{2} | . . . | α_{n}$
特别注意：

\begin{matrix} S \to a^{*} b (错误写法，没有Kleene闭包) \\ S \to A b \\ A \to A a | ε \end{matrix}

\begin{matrix} S \to a (b | c) (错 误 ， 没 有 括 号) \\ S \to a X \\ X \to b | c \end{matrix}

左递归： $A \to A α | β (l e f t r e c u r s i v e)$ 可表示 $β, β α, β α α . . .$ 即有推导 $A \Rightarrow^{*} β α^{n} (n = 0, 1, 2, . . .)$ 在EBNF中可表示为 $A \to β {α}$
右递归： $A \to α A | β (r i g h t r e c u r s i v e)$ 可表示 $β, α β, α β β . . .$ 即有推导 $A \Rightarrow^{*} α^{n} β (n = 0, 1, 2, . . .)$ 在EBNF中可表示为 $A \to {α} β$
结合性

\begin{matrix} e x p \to e x p a d d o p t e r m | t e r m \\ e x p \to t e r m {a d d o p t e r m} (左结合性) \\ e x p \to t e r m [a d d o p t e r m] (右结合性) \end{matrix}

中括号表示其中的符号出现0次或1次，大括号表示0次至无数次

推导(Derivation)与规约(Reduction)

如果能用一步步推导从初始符号得到需要验证的式子，那么式子就是符合规则的
推导就是不断用产生式的右部来替换一个非终止符
$\Rightarrow^{*}$ 表示多步推导
由终止符号构成的串称为句子(sentence)，由非终止符号构成的串是句型(sentential form)
以S为开始符号的CFG构成的语言： $L (G) = {s \in V_{T}^{*} | t h e r e e x i s t s S \Rightarrow^{*} s o f G}$

语法树

根节点是开始符号
内部节点是非终止符号
叶子节点是终止符号或者 $ε$
如果节点A有子节点 $X_{1}, X_{2}, . . ., X_{N}$ 则意为 $A \to X_{1} X_{2} . . . X_{N}$
最终的叶子节点连起来就是一个句子
不同的推导会得到不同的树，但是可能会有相同的结果。

最左推导(LeftMost Derivation前缀推导)

总是对句型中最左侧的非终止符号进行一次推导
从开始符号推导到结果，被称为Top-down

最右推导(RightMost Derivation)

从结果反向推回开始符号，这个过程被称为规约 $s \Rightarrow^{*} S$
等价于对语法树进行后序遍历的逆过程
最右推导的能力比最左推导要强

抽象语法树

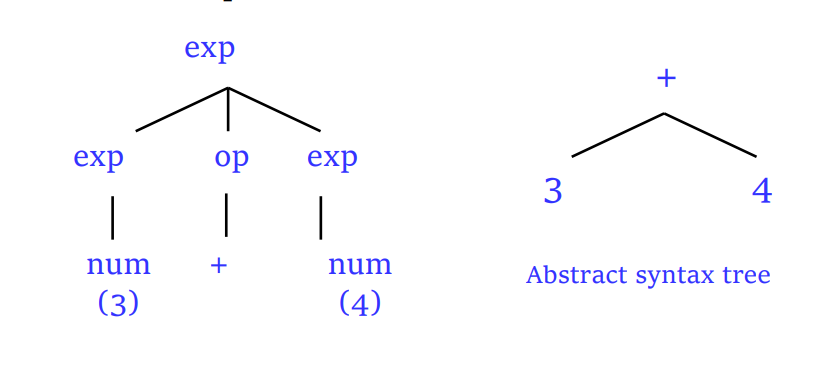
比起语法树，省略了部分细节，带来了更好的语法抽象，对于后续编译阶段是一个更好的数据结构
它反映了源码token序列的一个抽象，比语法树更高效

歧义(Ambiguity)

对于一个CFG，同样的输入可能有不同的解析

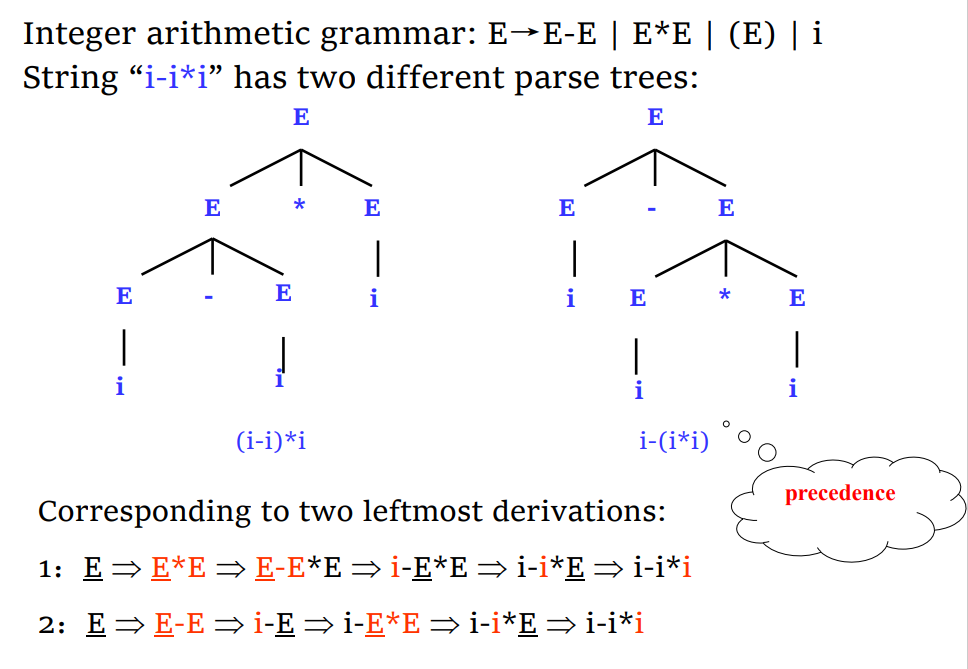
解决方法

消除歧义(Disambiguity rule)：不改变文法，列举所有可能造成歧义的情况并进行消除，不现实的
文法重写：改变文法，进行同义转换：(添加优先级，添加关联性)

E \to E - E | E \times E | (E) | i \Rightarrow \begin{matrix} E \to E - E | T \\ T \to T \times T | F \\ F \to (E) | i \end{matrix}

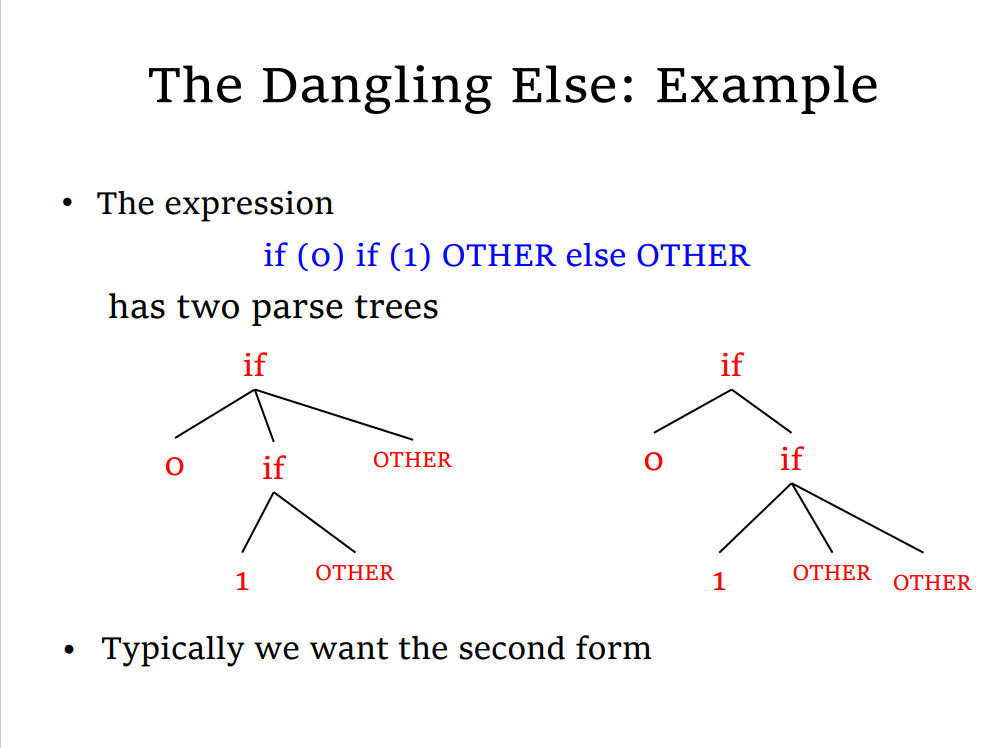
消除歧义1
消除歧义2
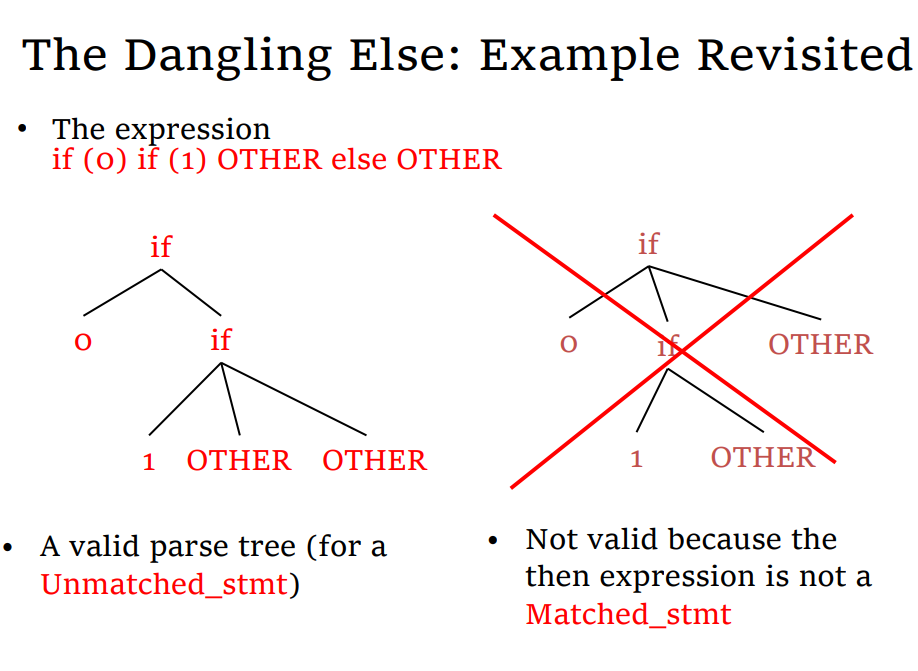
消除歧义3

语法分析算法(parsing)

Top-Down(Leftmost) parsing

本质上是一个图搜索问题，在树上搜索，查找能否获得一个与输入sentence匹配的路径

回溯算法(Backtracking)

用BFS：进行图遍历搜索，复杂，时间复杂度过高，产生大量无用分支，时间和空间的最差情况都是指数级别。现代编译器中不被使用
剪枝：由终止符号做前缀时，如果无法与输入的前缀匹配则剪枝。( $A a | A b | c \to c a a a a a$ 时，无法剪枝，因为前缀一直是非终止符号)
用DFS：有比BFS更好的空间复杂度和时间复杂度，但是无法匹配( $A a | c \to c$ ，因为会一直循环)

预测推导(predictive parsing)

Idea：利用先行词(lokkahead tokens)，也就是上面提到过的终止符前缀
两种分析方法：

递归下降分析(Recursive-descent parsing)
LL(1)分析

预测分析的概念

从输入串和文法的开始符号开始分析
可以从当前输入的token(s)唯一确定下一个要使用的产生式
预测分析文法包括LL(k)文法，其中L表示从左向右扫描，L表示最左推导，k表示“需要 $\leq k$ 个先行词用于预测 ”
LL(1)文法是常用的，也不完全常用

Lookahead Sets

First Sets(具体计算看讲义和书)

定义

\begin{matrix} G = (V_{N}, V_{T}, P, S) 是一个文法 \\ β \in (V_{N} \cup V_{T})^{*} \\ F I R S T (β) = {α \in V_{T} | β \Rightarrow^{*} a . . .} \\ i f β \Rightarrow^{*} ε t h e n ε \in F I R S T (β) \end{matrix}

计算

First()计算 3
First()计算 4
First()计算 5

//Todo 提取简练课程笔记

Follow Sets

定义：

\begin{matrix} G = (V_{N}, V_{T}, P, S) 是一个文法 \\ A \in V_{N} \\ F O L L O W (A) = {a \in V_{T} | S \Rightarrow^{*} . . . A a . . .}, \\ i f S \Rightarrow . . . A, t h e n $ \in F O L L O W (A) \\ $ 是 用 来 标 记 输 入 的 终 止 的 符 号 \end{matrix}

计算：

可空的非终止符(nullable nonterminal)

定义： $S \Rightarrow^{*} ε$

则称S是一个可空的非终止符

计算：

判定LL(1)文法

计算每个可空的非终止符
计算产生式右侧所有的 $F I R S T (α)$ 并验证其两两交集是否为空
计算(1)中算出的非终止符的 $F O L L O W (A)$ 并验证 $F I R S T (A) \cap F O L L O W (A) = \emptyset$

非LL(1)到LL(1)

两种简单的非LL(1)情形：

左因子，例如 $A \to α β | α r$ ，这是两个产生式的简写，其产生式交集为 $α$ ，改写方法为

\begin{matrix} A \to α β_{1} | α β_{2} | . . . | α β_{n} 重 写 为 : \\ A \to α A^{'} A^{^{'}} \to β_{1} | β_{2} | . . . | β_{n} \end{matrix}

左递归，包括直接左递归和间接左递归，例如 $A \to A β$ 和 $A \to B β B \to A α$ 改写方法为

\begin{matrix} A \to A α | β 重写为： \\ A \to β A^{^{'}}, A^{^{'}} \to α A^{^{'}} | ε \\ 一般情况为： \\ A \to A α_{1} | A α_{2} | . . . | A α_{m} | β_{1} | β_{2} | . . . | β_{n} 重写为： \\ A \to β_{1} A^{^{'}} | β_{2} A^{^{'}} | . . . | β_{n} A^{^{'}} \\ A^{^{'}} \to α_{1} A^{^{'}} | α_{1} A^{^{'}} | . . . | α_{m} A^{^{'}} | ε \end{matrix}

要注意：将这两者进行改写后并不能保证改写后的文法是LL(1)，仍需要再进行验证

递归下降

输入

非终止符号递归调用，终止符号匹配

int main(){
 Token token = getNextToken();
 S();/*S is the start symbol*/
 if(token!='$') throw error;
}
void A(){
 /*select a production of A:A→X_1X_2...X_k*/
 for(int i=0; i<k; k++){
  if(X[i].isnonterminal()) X[i]();
  else if(X[i]==input token) getNextToken();
  else throw error;
 }
}

如果 $U \to x_{1} | x_{2} | . . . | x_{n} 且 x_{1}, x_{2}, . . ., x_{n} \neq ε :$

void U(){
 if (token in First(x_1)) x_1();
 else if (token in First(x_2)) x_2();
 ...
 else if (token in First(x_n))x_n();
 else throw error;
}

如果 $U \to ε$ 则把

void U(){
 if(token in First(x_n))x_n();
 else throw error;
}

改写为：

void U(){
 if (token in First(x_n))x_n();
 else if(token not in Follow(x_n)) throw error;
}

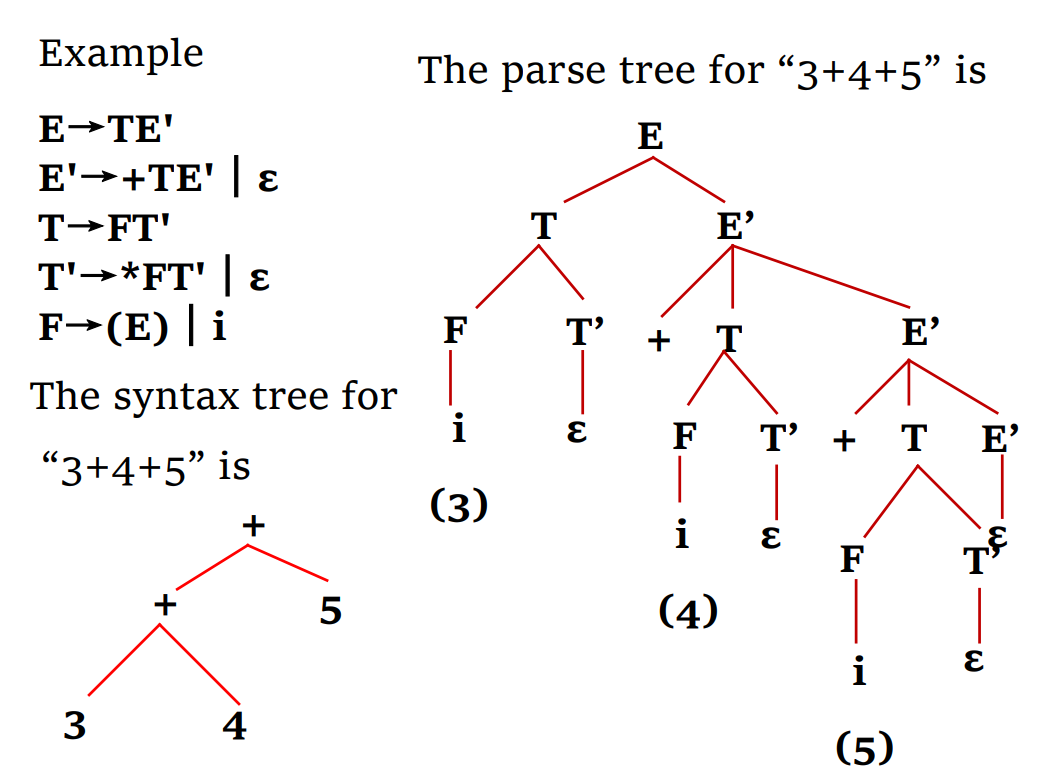
示例

递归下降示例1.png
递归下降示例2.png
递归下降示例3.png
递归下降示例4.png
递归下降示例5.png

输出(生成语法树)

语法树是一个中间表示
生成抽象语法树需要定义一个语义规则

优劣

优点：多功能，功能强大，简单有效；灵活，允许程序员安排操作，适用于手工生成的分析器
缺点：必须小心安排每个代码里的操作，而且递归操作会带来大量的时间复杂度和空间复杂度。

LL(1)

就是在递归下降的基础上用栈代替了递归，时间复杂度为 $O (n | G |) ， n 是字符串的长度， G 是语法的长度$
通过分析表(parsing table)来分析怎么转化一个非终止符号(如果不满足LL(1)文法，就会出现一个表项里有多个产生式)

产生分析表

分析表项 $M [N, t]$ 表示对于一个非终止符号N，当前输入token为t时，选择的产生式
构造分析表，对每个产生式 $A \to α$ 重复以下两步：
1. $对每个在 F I R S T [α]$ 中的 $t o k e n$ ，把产生式 $A \to α$ 加入表项 $M [A, a] 中$
2. 如果 $ε \in F i r s t (α)$ ，对 $F o l l o w (A) 中的每个元素(包括token和 $)$ ，把 $A \to α$ 加入表项 $M [A, a]$
- 从分析表的角度来说，一个不满足LL(1)文法的CFG文法产生的产生表的一个表项内可能有多个产生式，无法做到唯一选择

分析步骤

开始于把起始符号压入栈中；
把栈顶的非终止符号A用查表得到的产生式 $A \to α$ 替换；
当栈顶元素为终止符号后，将栈顶元素与输入匹配，匹配成功后，同时丢弃栈顶元素和输入元素
重复2、3步，直到输入和栈同时为空，则分析成功结束。

具体流程图(包括错误出现)：

示例：

错误处理

错误恢复(recovery)，在遇到错误时先恢复，让整个分析完成后再一起报错，而不是遇到一个报一个
错误修复(repair)：在出错后尝试修复

错误恢复

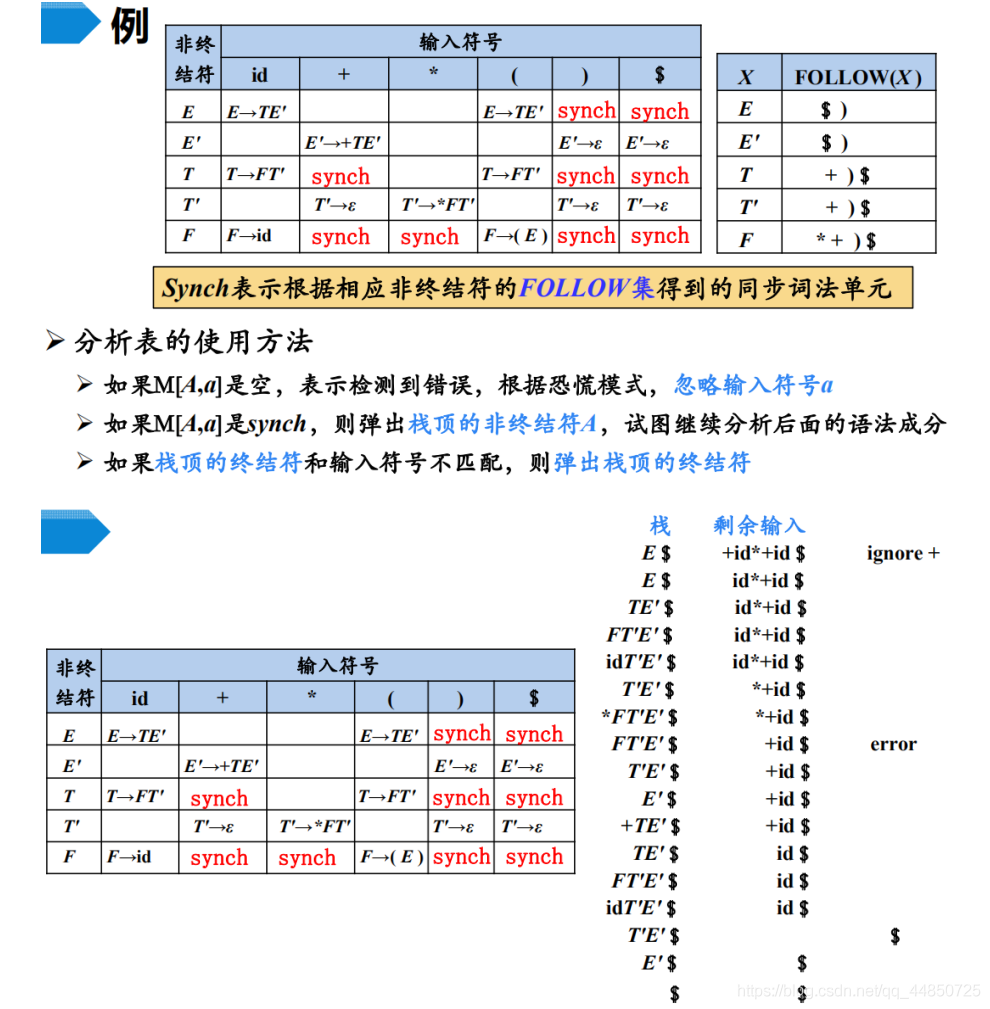
Panic Mode

不断尝试可能的token，如果能使得错误消失，那么就能继续分析了
通常从错误部分上下文的 $F O L L O W (优先) 和 F I R S T$ 集合中的token尝试

Bottom-up Parsing I

Handle

什么时候看到一个什么产生式的右部进行怎么样的规约(用哪个产生式)是Bottom-up算法的核心，而这个被归约的部分被称为handle，例如 $a A c d e \Rightarrow a A b c d e \Rightarrow a A c d e$ 中， $A b 是$ $a A b c d e 的 h a n d l e$
$h a n d l e$ 在右句型的左边(workarea)的最右边
从输入区移入语法分析栈(workarea)的过程称为shift，将栈中部分弹出并规约再入栈称为reduce
右句型(tight sentential Form): $S \Rightarrow^{*} S e n t e n t i a l F o r m$

Shift and Reduce Parsing

把分析栈成文右句型的可行前缀(viable prefix)
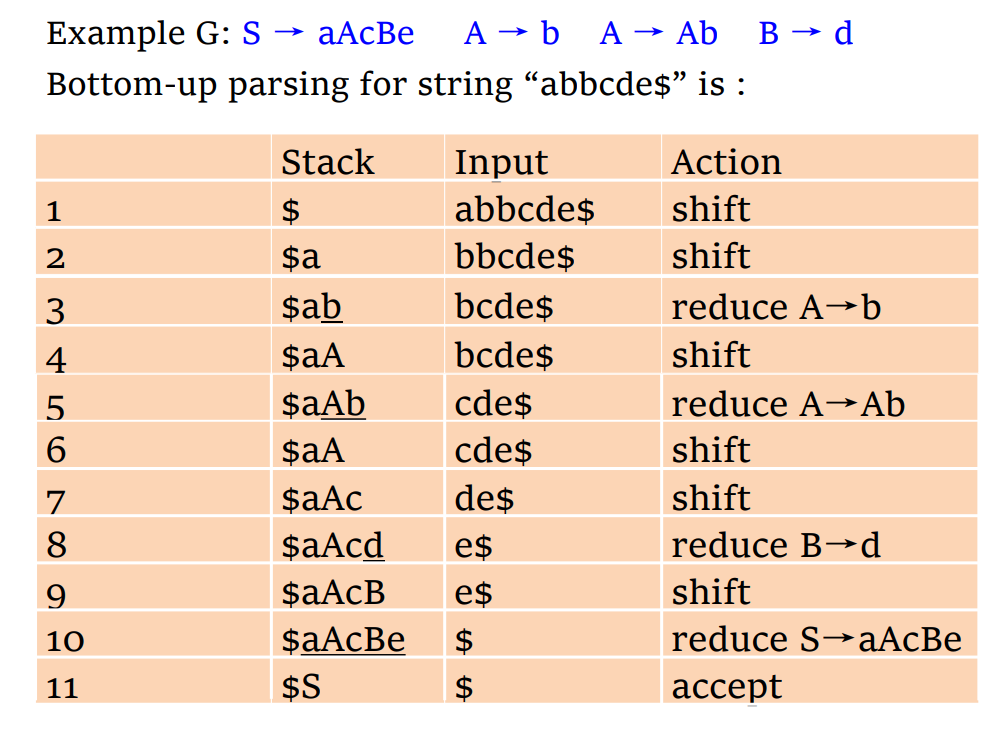
这种方法也被称为LR(0)，因为不需要lookahead token
但是LR算法需要看到栈顶以下多个元素，因此需要引入state来标记

LR Parsing

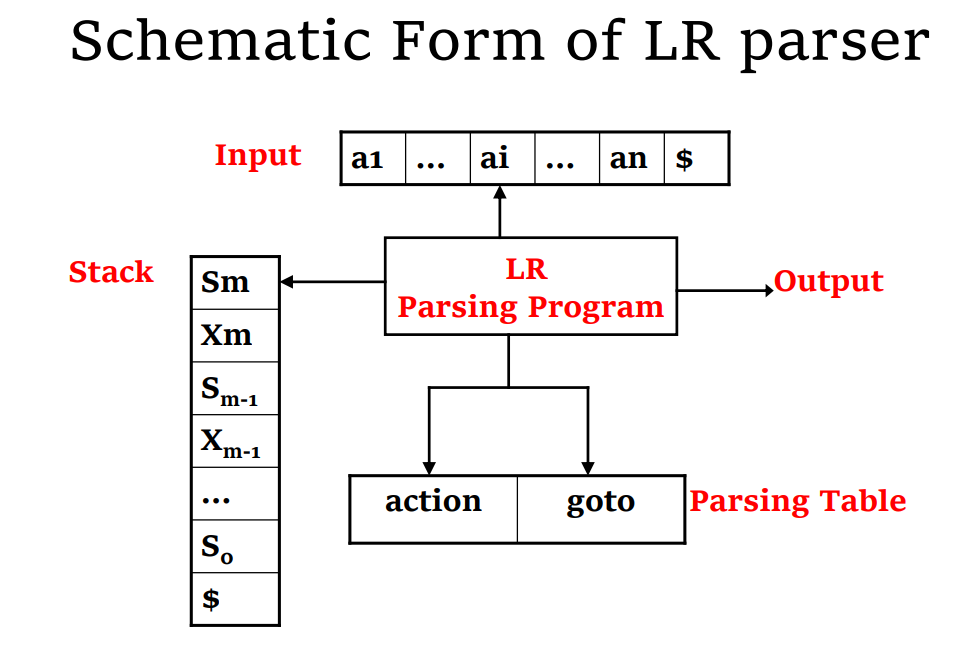
其中 $S_{m}$ 是状态， $X_{m}$ 是文法符号

Parsing Table

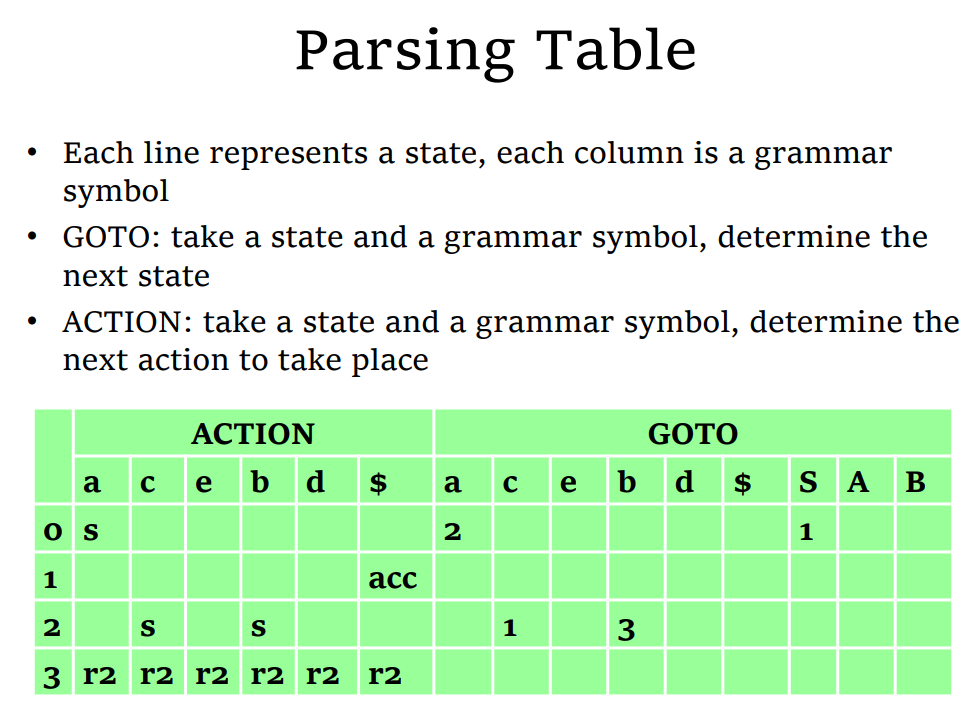
LR Parsing table.png
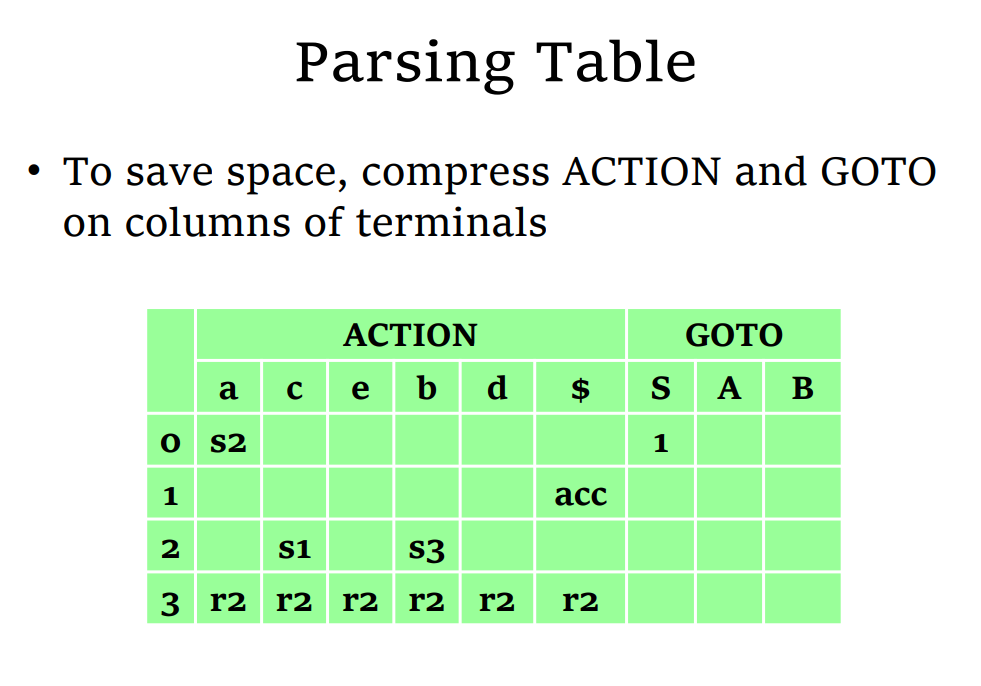
LR Parsing table2.png

对表项 $a c t i o n [S_{m}, a_{i}]$ ：
- Shift( $s_{k}$ )表示把对应的标识符 $S_{m}$ 和状态 $s_{k}$ 从输入移入到分析栈中
- Reduction( $r_{k}$ )表示用第 $k$ 个产生式( $A \to γ$ )进行规约，这个步骤包括：
  1. 把 $γ 串$ 对应的所有字符和状态从栈中弹出，假设弹出后栈顶状态位 $s_{i}$
  2. 把非终止符号A入栈
  3. 把状态 $S_{j} = G O T O [S_{i}, A] 入栈$
Accept：表示分析顺利结束
Error：表示分析遇到了某些问题

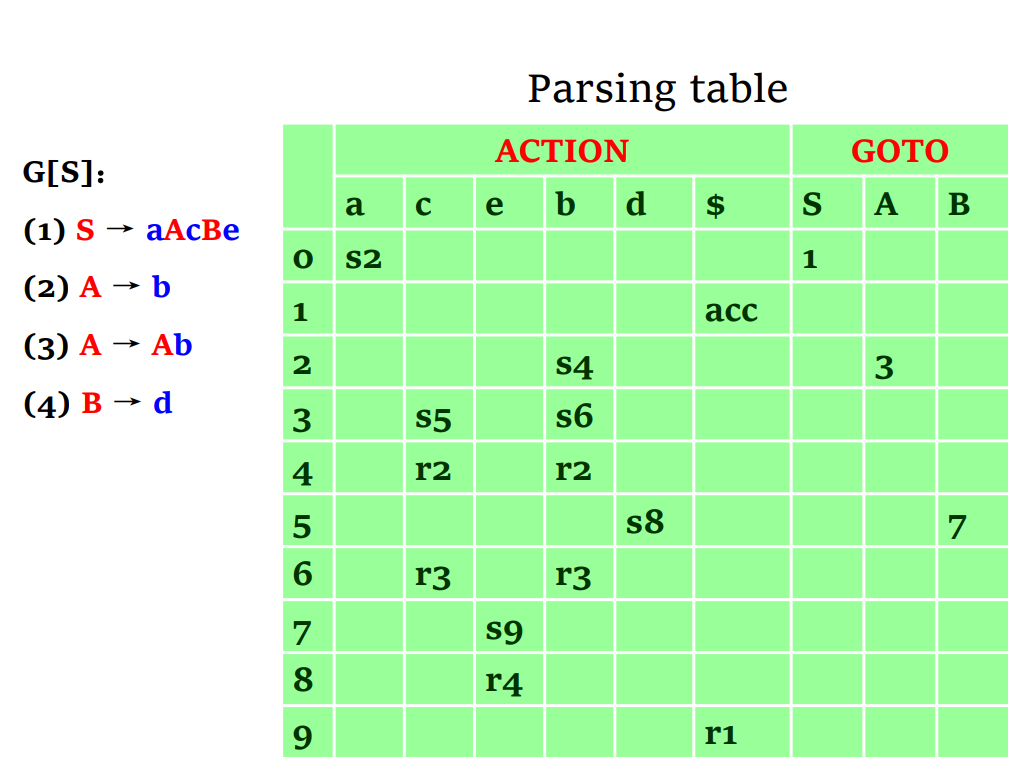
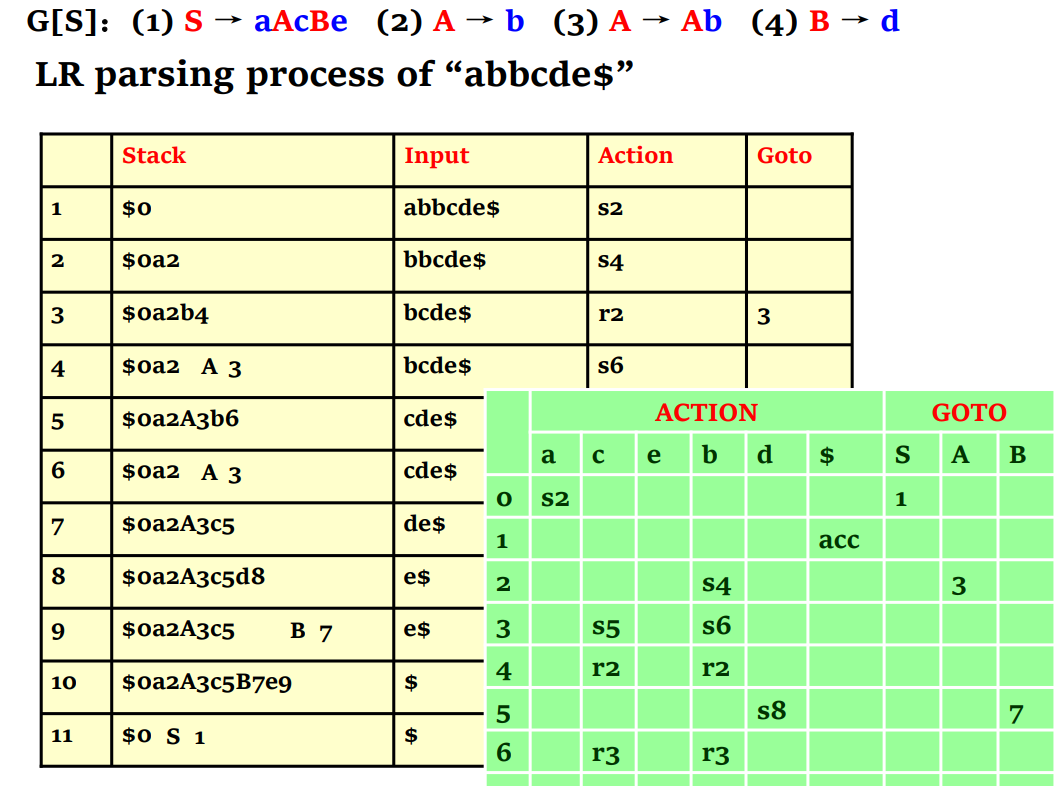
LR(0) items and parsing table

LR(0) items

一个语法G的LR(0)项就是G的产生式再在其右侧加上一个位置点
例如 $U \to X Y Z$ 有四种形式： $[0] U \to \cdot X Y Z$ $[3] U \to X Y Z \cdot$ (被称为完成项)
$U \to X \cdot Y Z$ 和 $T \to X \cdot A B$ 可以归成一个项集，用一个state刻画，在栈中用 $X_{m}$ 来区分这两个项

Items 的自动机形式

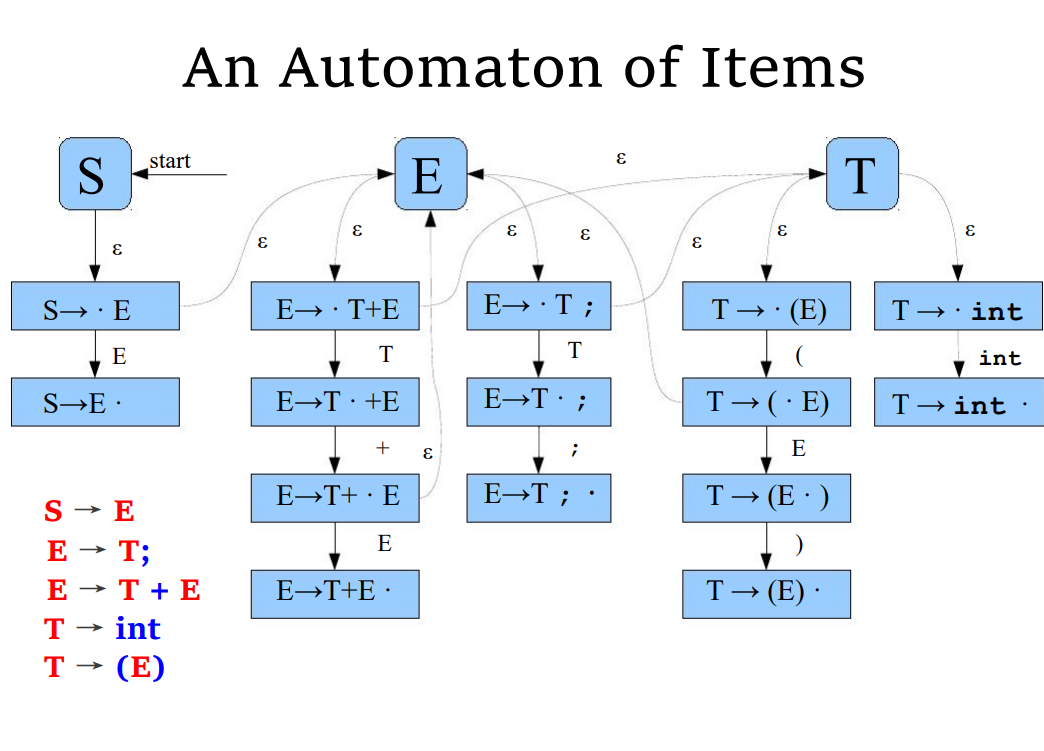
构建NFA

每个状态是一个项
几乎用不上不用了解

构建DFA

每个状态是一个项集

增广(augment)：如果原来的文法的开始符号没有做为一个产生式的右部，就新增一个产生式 $S \to E$ 其中 $E$ 就是原来的开始符号
构建开始状态：把每个产生式都加入初始状态
构造转移：对项集中的每个项，看输入符号后位置点会不会后移，是的话就构造一个转移和对应的项集，并把其 $ε$ 闭包加入项集，把完成项作为accepting state
不断重复2，3，把增广产生式存在的项集作为接受状态

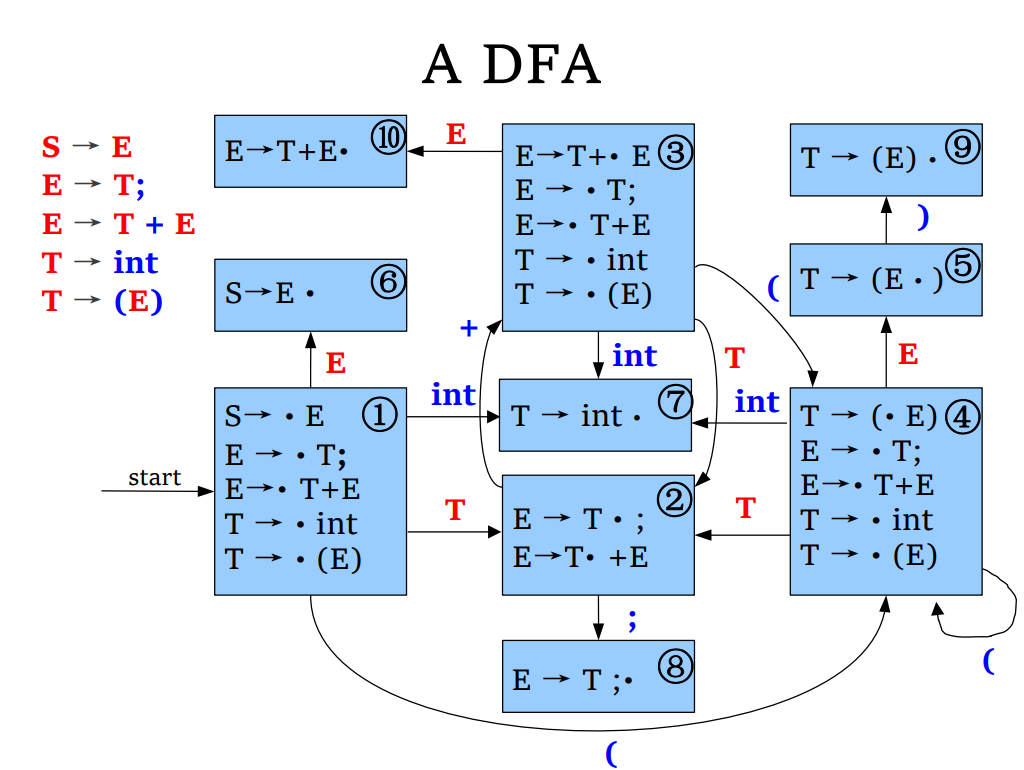
构建LR(0) Parsing Table

构建DFA
构建state K 对应的ACTION：如果 $A \to α \cdot β \in K$ ,则 $A C T I O N [K] = S h i f t$ 如果 $A \to α \cdot \in K$ , 并且 $A \to α$ 需要 $j$ 个栈中元素，那么 $A C T I O N [K] = R_{j}$

LR(0)的限制

LR(0)的自动机中有完成项的项集只能有完成项，否则会出现shift/reduce冲突(同时有完成项和非完成项)或reduce/reduce冲突(有多个完成项)

Bottom-UP Parsing II

SLR(1)(Simple LR(1))

SLR(1)文法

simple在使用的仍然是LR(0)的DFA

对于一个状态 $I = {X \to α \cdot b β, A \to r \cdot, B \to δ \cdot}$ 其中 $b \in V_{T}$ 如果 $F o l l o w (A) \cap F o l l o w (B) = \emptyset$ 且不包含 $b$ 那么 $I$ 的下一个行动取决于下一个输入的token $^{'} a^{'}$