基本概念
- 索引机制用于加速对所需数据的访问。例如,图书馆中的作者目录。
- 搜索键(Search Key)是用于在文件中查找记录的一组属性。
- 索引文件由记录(称为索引条目)组成,形式为:
| search-key | pointer |
|---|
- 索引文件通常比原始文件小得多。
- 基本的两种索引类型:
- 有序索引(Ordered indices):搜索键按排序顺序存储。
- 哈希索引(Hash indices):使用“哈希函数”,将搜索键均匀分布在“桶”中。
有序索引(Ordered Indices)
- 在有序索引中,索引条目按照搜索键值进行排序。例如,图书馆中的作者目录。
- 主索引(Primary index):在顺序有序文件中,其搜索键指定文件的顺序。
- 也称为聚集索引(clustering index)。
- 主索引的搜索键通常是主键,但不一定是。
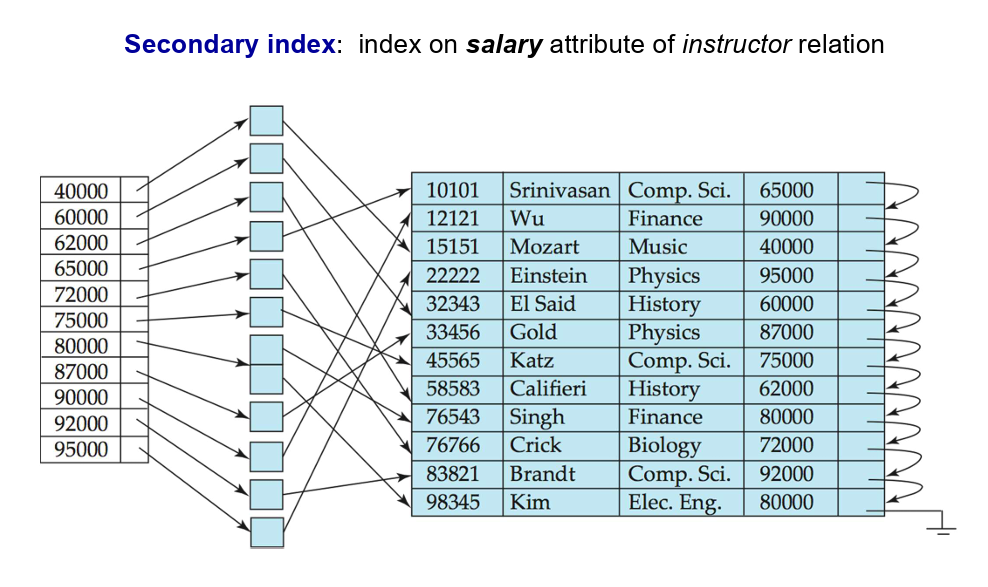
- 次索引(Secondary index):其搜索键指定与文件的顺序不同的顺序的索引。也称为非聚集索引(non-clustering index)。
- 索引顺序文件:带有主索引的有序顺序文件(Index-sequential file)。
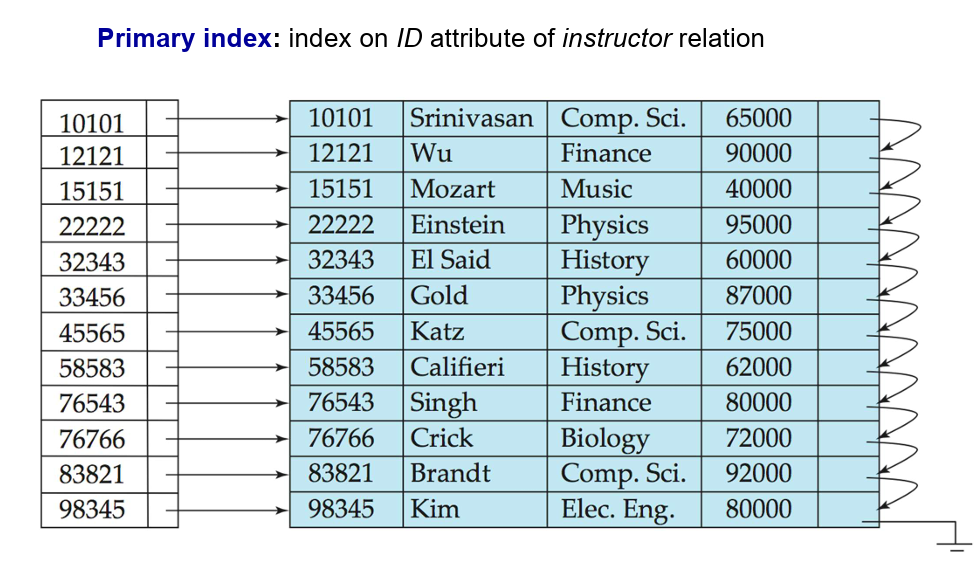
稠密索引文件(Dense Index Files)
- 稠密索引(Dense Index):在文件中的每个搜索键值都出现索引记录。
例如,教师关系的 ID 属性上的索引。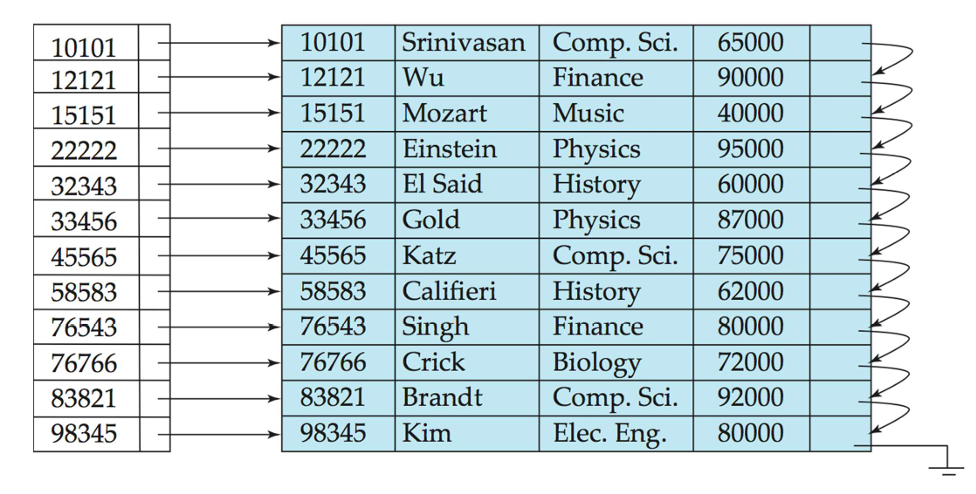
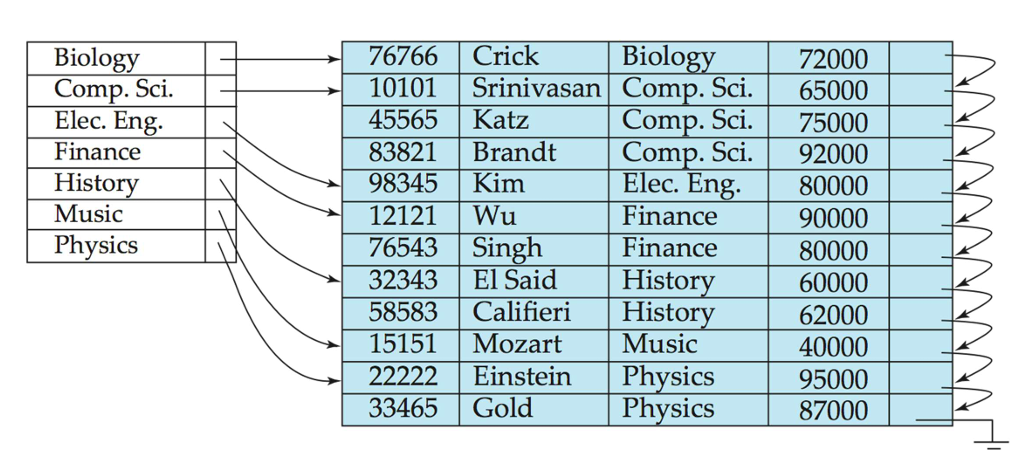
稀疏索引文件(Sparse Index Files)
- 稀疏索引(Sparse Index):仅包含某些搜索键值的索引记录。
- 适用于记录按搜索键顺序排列的情况。
- 要找到具有搜索键值 K 的记录,我们:
- 找到最大的搜索键值小于 K 的索引记录。
- 从索引记录指向的记录开始,在文件中顺序查找。
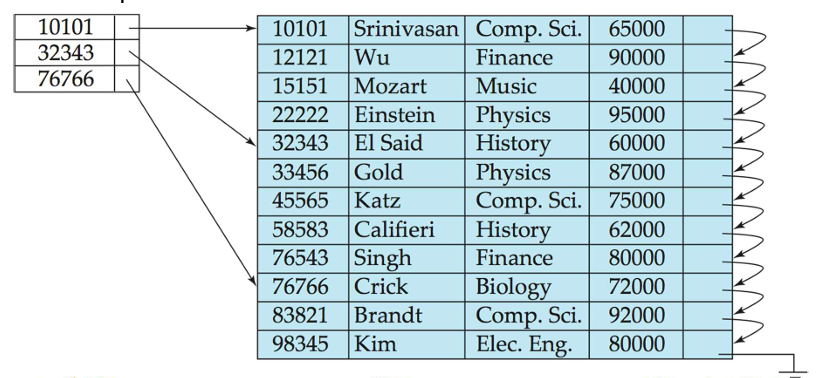
- 与稠密索引相比:
- 占用更少的空间,并且插入和删除的维护开销更小。
- 通常比稠密索引定位记录的速度较慢。
- 良好的权衡:稀疏索引中每个块对应一个索引条目,对应于块中最小的搜索键值。
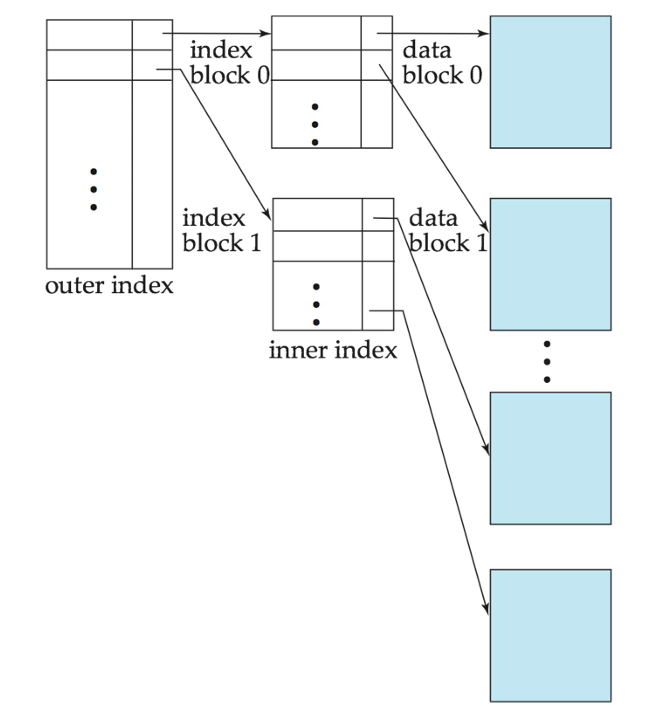
多级索引(Multilevel Index)
- 如果主索引无法放入内存中,访问将变得昂贵。
- 解决方案:将保存在磁盘上的主索引视为顺序文件,并在其上构建一个稀疏索引。
- 外部索引 - 主索引的稀疏索引
- 内部索引 - 主索引文件
- 如果即使外部索引也太大无法放入主存储器中,可以创建另一级索引,依此类推。
- 所有级别的索引在对文件进行插入或删除时必须进行更新。
索引的增删
- 单级索引条目删除:
- 稠密索引:删除搜索键类似于删除文件记录。
- 稀疏索引:
- 如果索引中存在搜索键的条目,则通过用文件中的下一个搜索键值(按搜索键顺序)替换索引中的条目来删除它。
- 如果下一个搜索键值已经有索引条目,则删除该条目而不是替换它。
- 单级索引插入:
- 使用要插入的记录中出现的搜索键值进行查找。
- 稠密索引:如果搜索键值在索引中不存在,则插入它。
- 稀疏索引:如果索引对文件的每个块存储一个条目,除非创建新的块,否则无需对索引进行任何更改。
- 如果创建了新的块,则将新块中出现的第一个搜索键值插入索引中。
- 多级插入和删除:算法是单级算法的简单扩展。
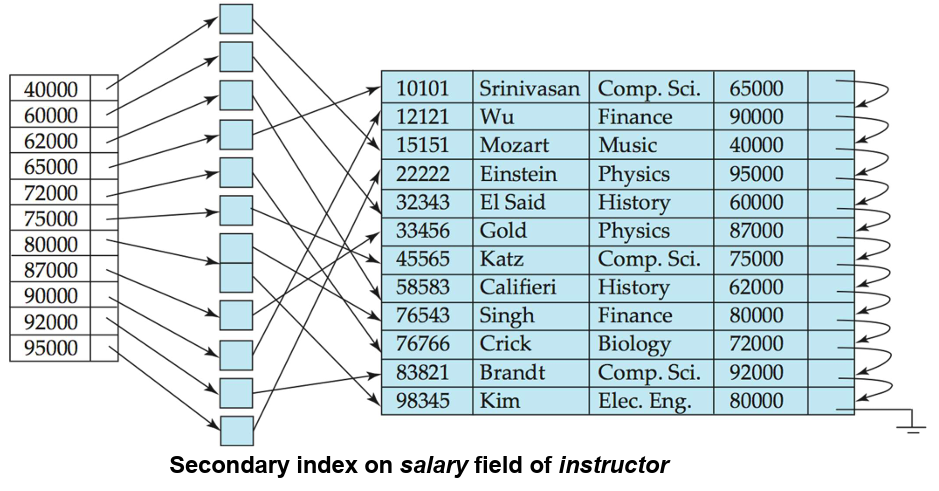
次索引(Secondary index)
- 索引记录指向一个桶(bucket),该桶包含指向具有特定搜索键值的所有实际记录的指针。
- 次级索引必须是稠密索引。
相关信息
- 索引在搜索记录时提供了显著的好处。
- 但是,更新索引会对数据库修改施加开销 - 当文件被修改时,必须更新文件上的每个索引。
- 使用主索引进行顺序扫描是高效的,但使用次级索引进行顺序扫描是昂贵的。
- 每次记录访问可能需要从磁盘中获取一个新的块。
- 块获取大约需要 5 到 10 毫秒的时间,而内存访问大约需要 100 纳秒的时间。
:::
B+树索引文件(B+ Tree Index Files)
- B+树索引是索引顺序文件的一种替代方案
- 索引顺序文件的缺点:
- 随着文件的增长,性能会下降,因为会创建许多溢出块。
- 需要定期对整个文件进行重新组织。
- B+树索引文件的优势:
- 在插入和删除操作中,可以自动进行小范围、局部的重新组织,无需对整个文件进行重新组织以保持性能。
- B+树的(轻微)缺点:
- 插入和删除操作的开销略大,存在空间开销。
- B+树的优势超过了缺点,因此被广泛使用。
- B 树是满足以下属性的根树:
- 从根到叶子的所有路径长度相同。
- 内部节点(不是根节点或叶子节点):具有
- 叶子节点:具有
- 根节点:
- 如果不是叶子节点,则至少有
- 如果是叶子节点,则可以有
- 如果不是叶子节点,则至少有
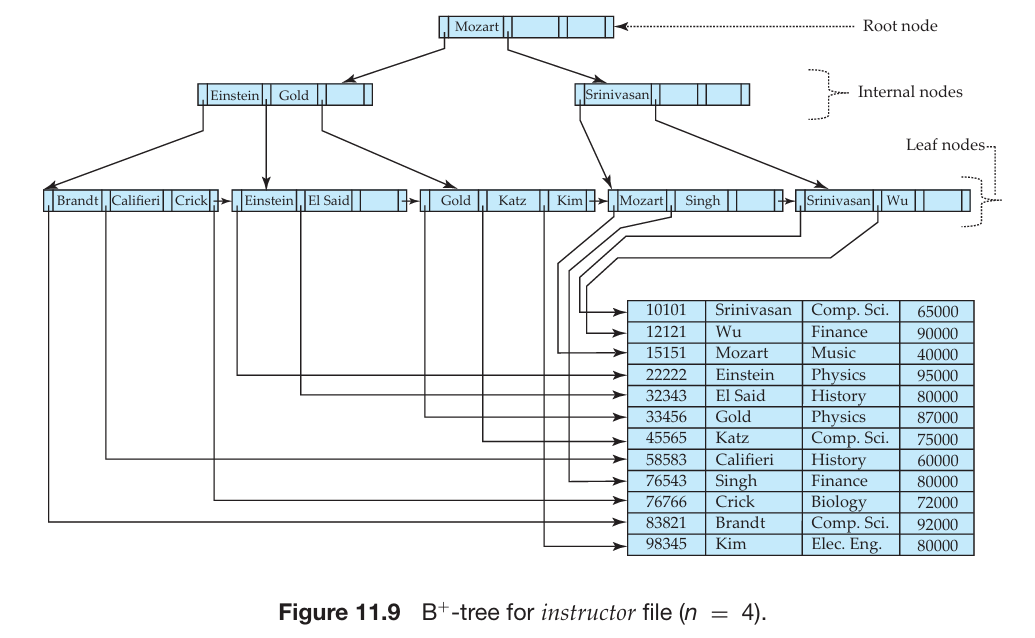
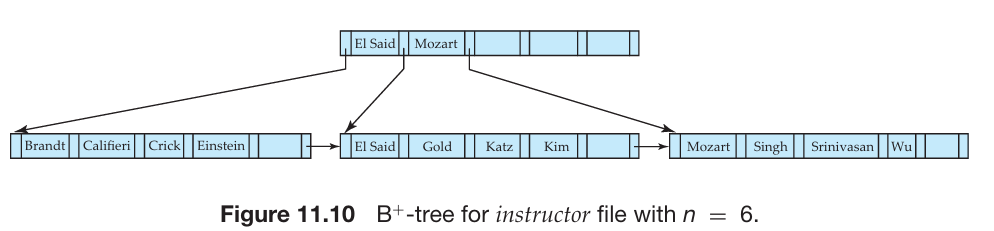
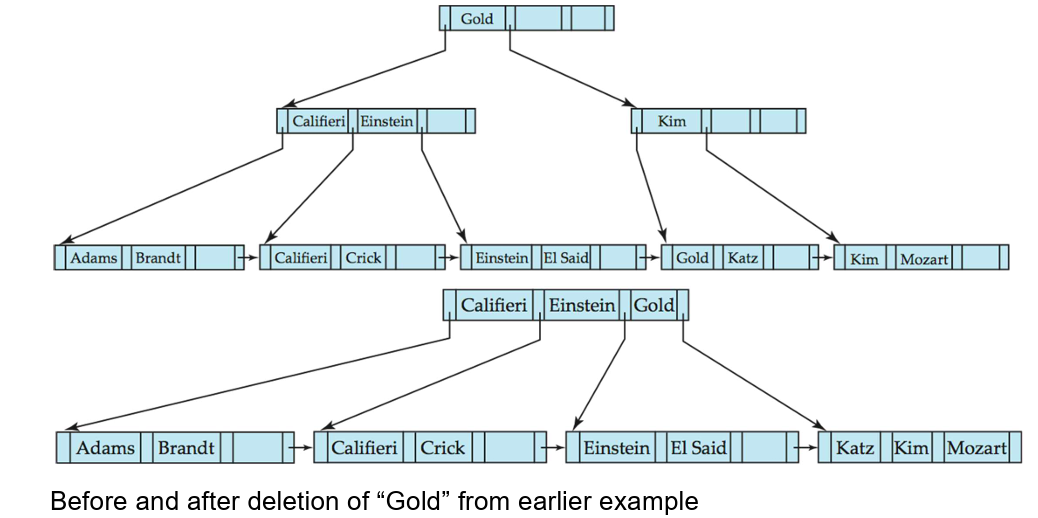
- 例如下图所示:
- 叶子节点必须有 3 到 5 个值(⌈(n–1)/2⌉和 n–1,其中 n = 6)。
- 非根的非叶子节点必须有 3 到 6 个子节点(⌈n/2⌉和 n,其中 n = 6)。
- 根节点必须至少有 2 个子节点。
B+ 树的节点结构

- 在非叶子节点中,它们是指向子节点的指针。
- 在叶子节点中,它们是指向记录或记录桶的指针。
- 节点中的搜索键按顺序排列:
(最初假设没有重复的键,稍后处理重复键的情况) - 叶子节点满足:
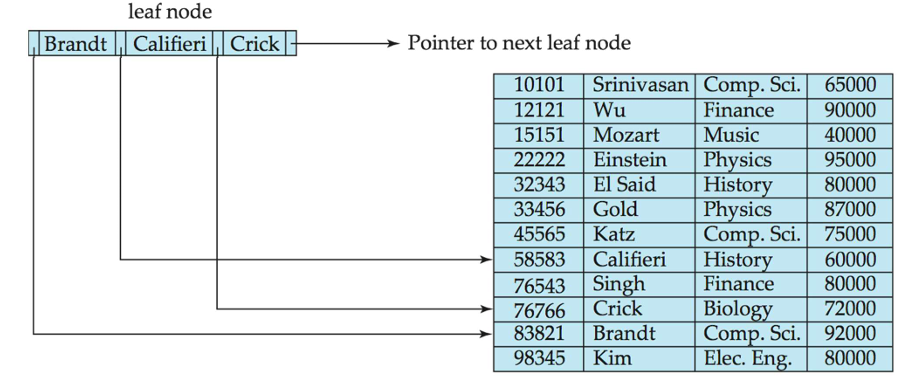
- 非叶子节点满足:
相关信息
- 由于节点之间的连接是通过指针完成的,"逻辑上"接近的块(查找关键字的值相近)和"物理上"接近的块(磁盘地址相近)不一定需要在索引中相邻。
- 例如:Einstein 和 Gold
- B+树的非叶子节点实际上构成了一个稀疏索引的架构
:::
B+树的高度
- B+树包含相对较少的级别。
- 根节点下面的级别至少有
- 下一级至少有
- 依此类推。
- 根节点下面的级别至少有
- 如果文件中有 m 个搜索键值,则树的高度不超过
- 主文件的插入和删除操作可以高效处理,因为索引可以在对数时间内重新结构(后面将会看到)。
在 B+树中进行查询
查找具有搜索键值 V 的记录:
- 将
- 当
- 找到最小的索引
- 如果不存在这样的索引 i,则将 C 设为 C 中的最后一个非空指针。
- 否则,如果
- 否则,如果
- 找到最小的索引
- 令
- 如果存在这样的值
- 否则,不存在具有搜索键值
- 如果存在这样的值
B+树性能
- 如果文件中有
- 一个节点通常与一个磁盘块的大小相同,通常为 4 千字节。
- 对于有 100 万(
- 与具有 100 万搜索键值的平衡二叉树相比,查找操作中访问约 20 个节点。
- 上述差异非常显著,因为每次节点访问可能需要进行磁盘 I/O,耗费约 20 毫秒的时间。
B+树文件组织
- 使用 B+树索引解决了索引文件退化问题。
- 使用 B+树文件组织解决了数据文件退化问题。
- B+树文件组织中,B+树的叶子节点存储记录,而不是指针。
- 叶子节点仍需要保持至少半满。
- 由于记录比指针更大,叶子节点中可以存储的记录数目少于非叶子节点中的指针数目。
- 插入和删除的处理方式与 B+树索引中的插入和删除条目相同。
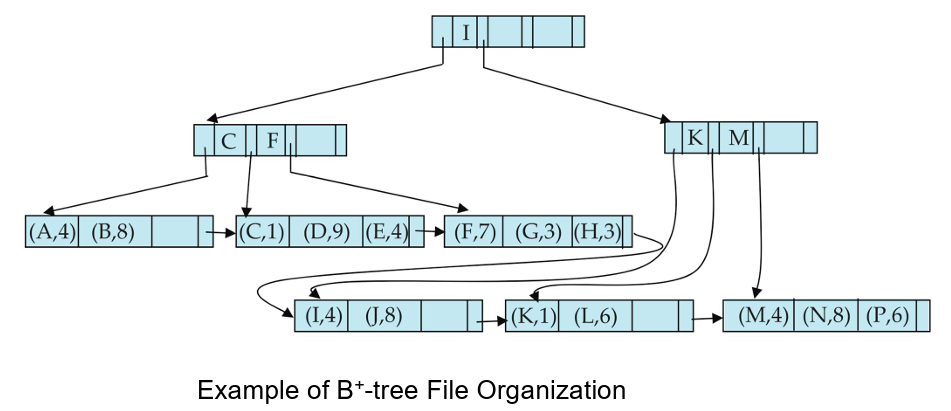
- 通过对两个兄弟节点的重新分配(尽可能避免拆分/合并),来确保每个节点至少有
- 不同节点的子节点数目差异巨大的原因是:
- 节点的物理大小是固定的,而键值的大小是可变的。
- 在拆分过程中,使用空间利用率作为判据,而不是指针的数量。
- 前缀压缩:
- 内部节点的键值可以是完整键值的前缀。
- 保留足够的字符来区分由键值分隔的子树中的条目。例如,"Silas"和"Silberschatz"可以通过"Silb"分隔。
- 叶子节点中的键值可以通过共享公共前缀来进行压缩。
多键索引(Indices on Multiple Keys)
- 对于某些类型的查询,可以使用多个索引。例如:
- 从 instructor 表中选择 ID,其中 dept_name = "Finance"且 salary = 80000。
- 处理使用单个属性索引的查询的可能策略:
- 使用 dept_name 索引找到部门名称为"Finance"的教师,然后检查 salary 是否为 80000。
- 使用 salary 索引找到薪水为 80000 的教师,然后检查 dept_name 是否为"Finance"。
- 使用 dept_name 索引找到与"Finance"部门相关的所有记录的指针,类似地,使用 salary 索引。取两组指针的交集。
- 假设我们有一个组合搜索键(dept_name,salary)的索引。
- 对于 where 子句 where dept_name = "Finance" and salary = 80000,
- 索引(dept_name,salary)可以仅用于获取满足两个条件的记录。
使用单独的索引效率较低-可能会获取满足其中一个条件的许多记录(或指针)。 - 还可以高效处理 where 子句 where dept_name = "Finance" and salary < 80000。
- 但是不能高效处理 where 子句 where dept_name < "Finance" and balance = 80000。
- 可能会获取满足第一个条件但不满足第二个条件的许多记录。
B+树的插入
- 分裂叶子节点:
- 按照排序顺序获取
- 在被分裂的节点的父节点中插入
- 如果父节点已满,将其分裂并向上传播分裂。
- 节点的分裂向上进行,直到找到一个不满的节点。在最坏的情况下,根节点可能会分裂,将树的高度增加 1。
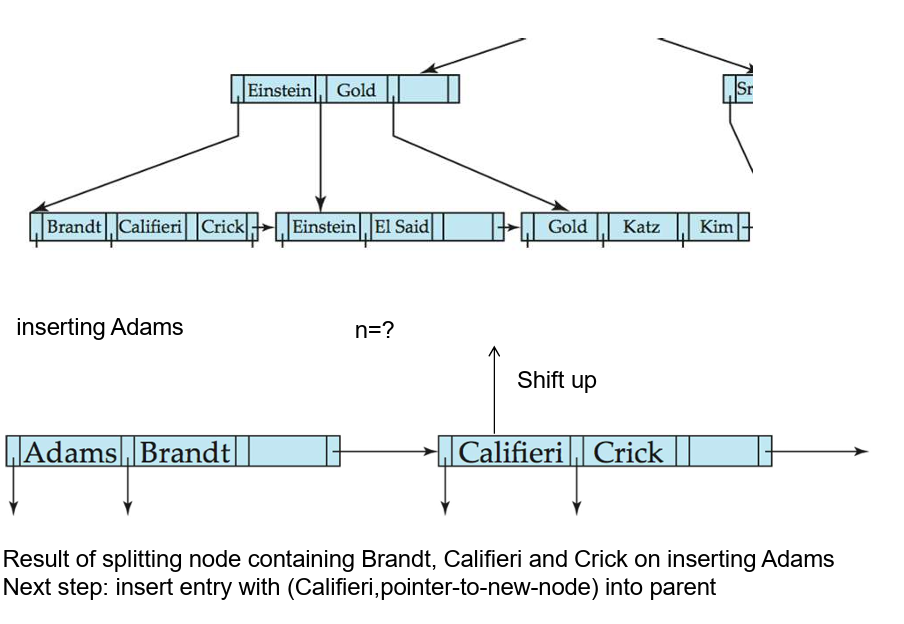
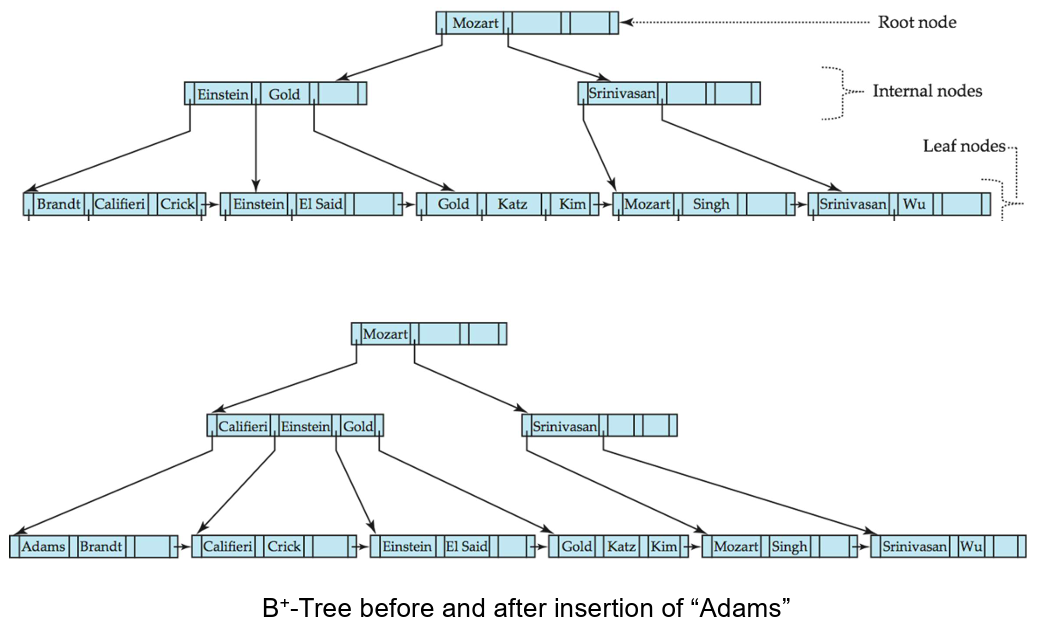
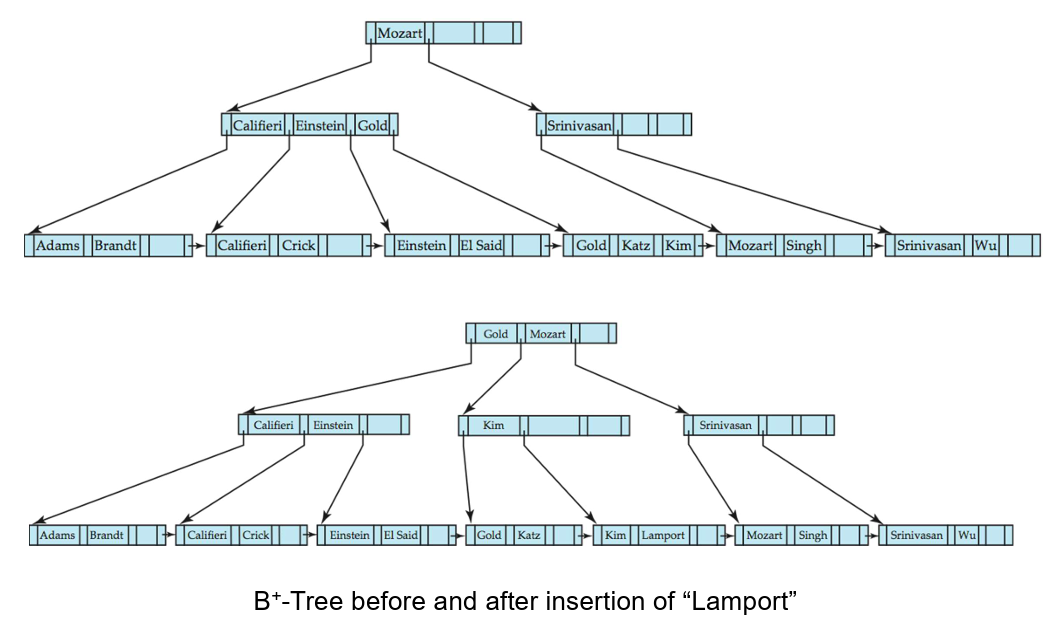
- 按照排序顺序获取
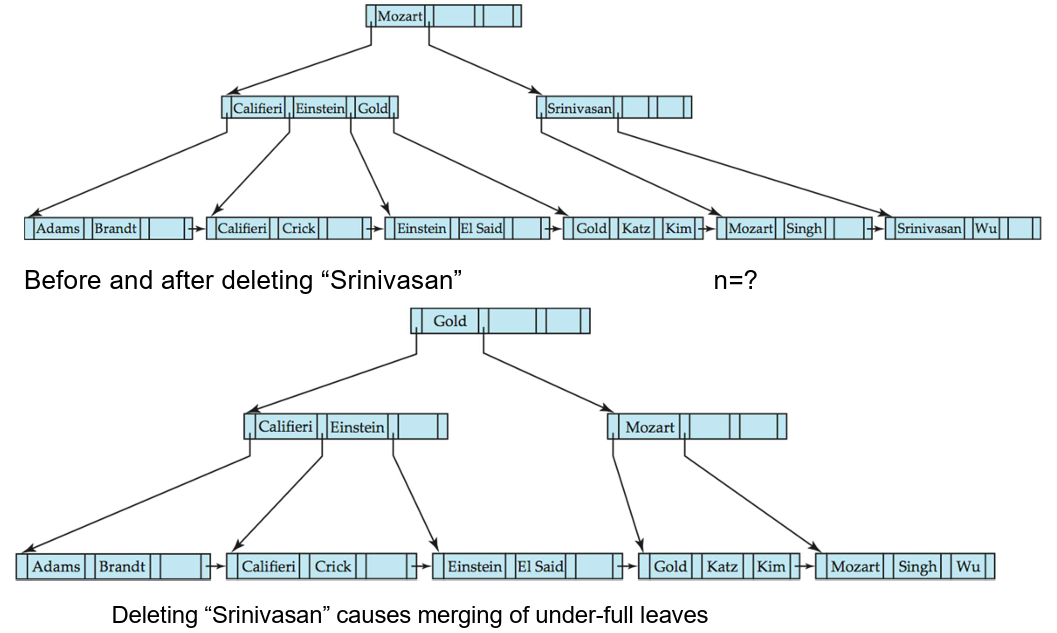
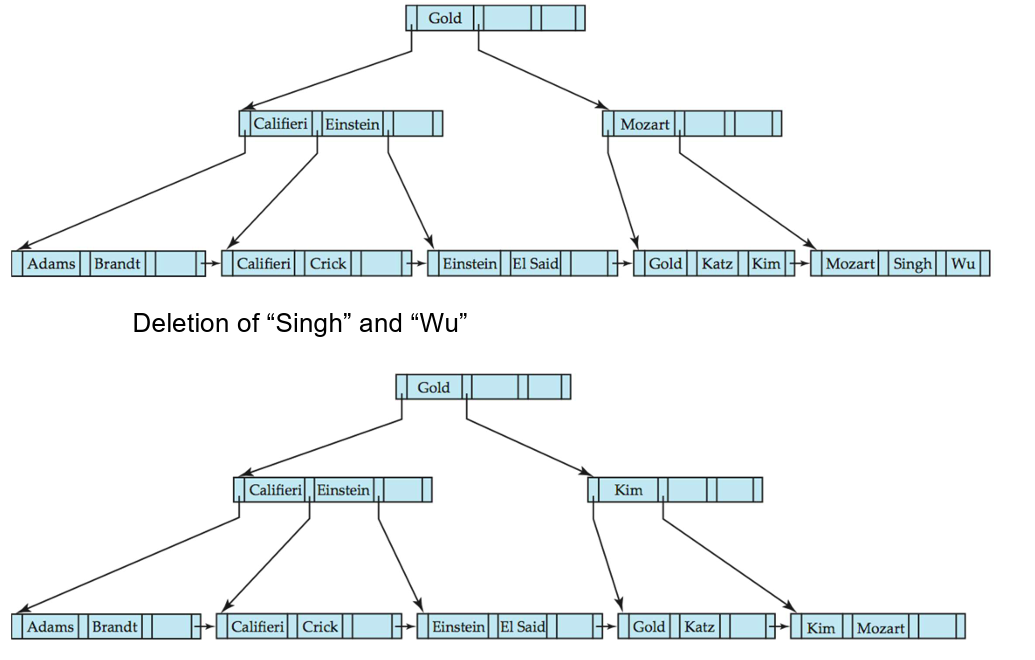
B+树的删除
- 如果由于删除操作导致节点中的条目过少,
- 情况(1):节点中的条目和一个兄弟节点可以放入一个单一节点中,那么进行
合并操作(merge siblings):- 将两个节点中的所有搜索键值插入一个单一节点(左边的节点),并删除另一个节点。
- 从父节点中递归地删除键值对
- 情况(2):节点中的条目和一个兄弟节点无法放入一个单一节点中,那么进行
重新分配指针操作(redistribute pointers):- 在节点和一个兄弟节点之间重新分配指针,使得两者都有超过最小条目数。
- 更新节点的父节点中相应的搜索键值。
- 情况(1):节点中的条目和一个兄弟节点可以放入一个单一节点中,那么进行
- 节点删除可能会向上级联,直到找到一个具有
- 如果根节点在删除后只剩下一个指针,那么根节点将被删除,唯一的子节点将成为新的根节点。
哈希(Hashing)
静态哈希
- 一个桶(bucket)是一个存储单元,包含一个或多个记录(通常是一个磁盘块)。
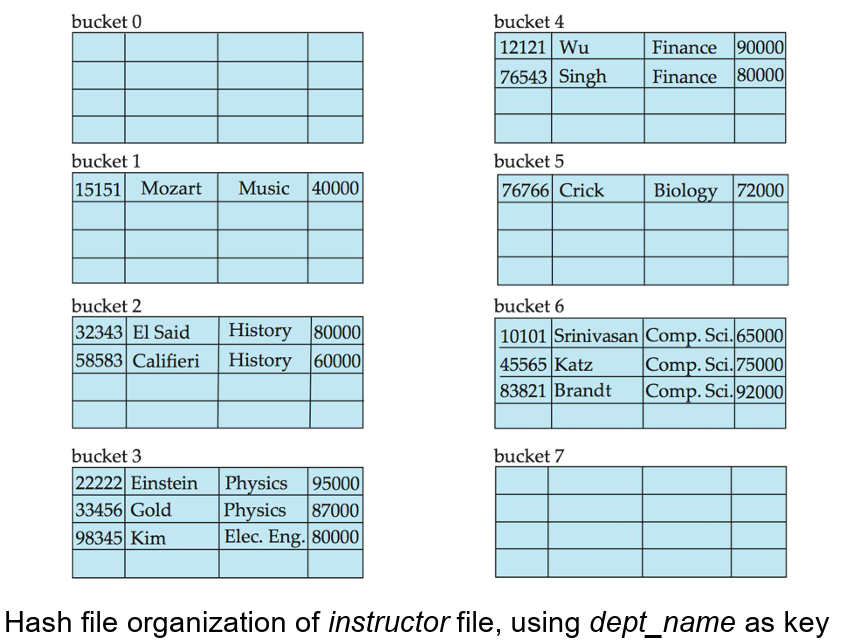
- 在哈希文件组织中,我们通过哈希函数直接从搜索键值获取记录所在的桶。
- 哈希函数
- 哈希函数用于定位记录的访问、插入和删除。
- 具有不同搜索键值的记录可能映射到同一个桶中,因此必须顺序地搜索整个桶以定位记录。
- 例如下图所示是用
哈希函数
- 最差的哈希函数将所有的搜索键值映射到同一个桶中,这会导致访问时间与文件中搜索键值的数量成正比。
- 理想的哈希函数是均匀(uniform)的,即每个桶从所有可能的值中分配相同数量的搜索键值。
- 理想的哈希函数是随机(random)的,因此每个桶中分配给它的记录数量相同,不受文件中搜索键值实际分布的影响。
- 典型的哈希函数对搜索键的内部二进制表示进行计算。
- 例如,对于字符串搜索键:
- 可以计算字符串中所有字符的二进制表示的和。
- 哈希值是和除以桶的数量后的余数。
- 例如,对于字符串搜索键:
处理桶溢出
- 桶溢出可能发生的原因:
- 桶数量不足
- 偏斜(skew):记录的分布不均匀。这可能是因为两个原因:
- 不随机:多个记录具有相同的搜索键值
- 不均匀:选择的哈希函数导致键值的分布不均匀
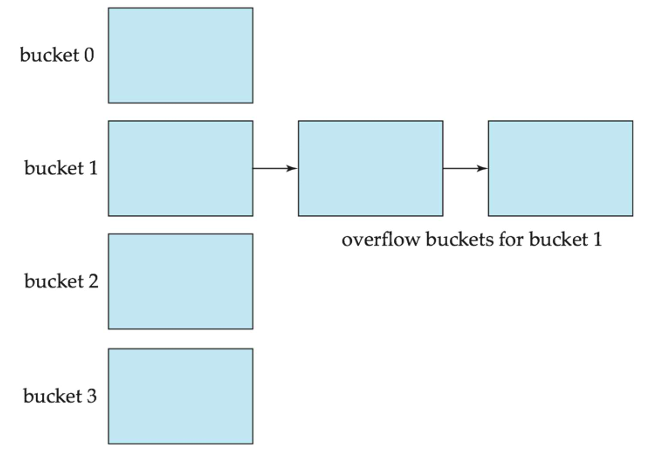
- 尽管可以减少桶溢出的概率,但无法完全消除;它通过使用溢出桶(overflow buckets)来处理。
- 溢出链表法:给定桶的溢出桶通过链表连接在一起。又被称为闭散列/闭哈希(Closed Hashing)
- 另一种称为开放散列(Open Hashing)的替代方案不使用溢出桶,但对数据库应用不适用。
哈希索引(Hash Indices)
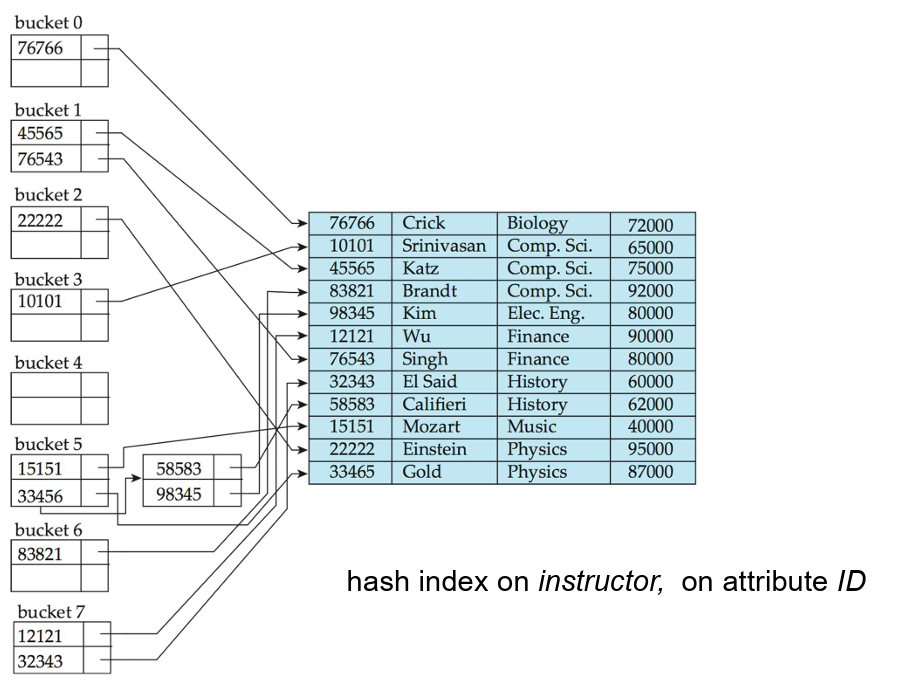
- 哈希不仅可以用于文件组织,还可以用于索引结构的创建。
- 哈希索引将搜索键与其关联的记录指针组织成一个哈希文件结构。
- 严格来说,那么哈希索引始终是次要索引。
- 如果文件本身使用哈希进行组织,在使用相同的搜索键进行哈希的情况下,对其创建单独的主要哈希索引是不必要的。
- 然而,我们使用术语哈希索引来指代次要索引结构和哈希组织的文件。
静态哈希的不足之处
- 在静态哈希中,哈希函数 h 将搜索键值映射到一个固定的桶地址集合 B。数据库随着时间的推移而增长或缩小。
- 如果初始桶的数量过小,并且文件不断增长,由于溢出过多,性能将下降。
- 如果为预期增长分配空间,最初将浪费大量空间(桶将不充分)。
- 如果数据库缩小,同样会浪费空间。
- 一种解决方案是定期使用新的哈希函数对文件进行重新组织,但这种方法昂贵,会干扰正常操作。
- 更好的解决方案是允许动态修改桶的数量。
比较顺序索引和哈希索引
定期重新组织的成本
插入和删除的相对频率
期望的查询类型:
- 哈希通常更适合检索具有指定键值的记录。
- 如果范围查询很常见,最好选择有序索引。
在实践中:
- PostgreSQL 支持哈希索引,但由于性能较差,不鼓励使用。
- Oracle 支持 B+树、位图等。
- SQLServer 仅支持 B+树。
